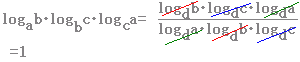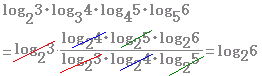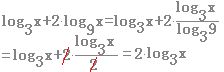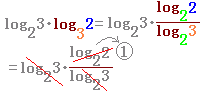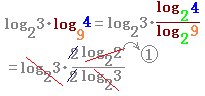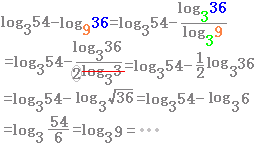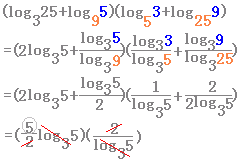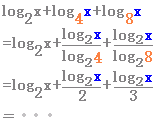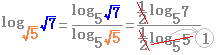|
← PC�p�͕ʕ�
��ΐ��̒�`��
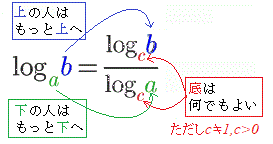
�w�����Ƒΐ����̊W (�w���̌`)�@�@(�ΐ��̌`)
��ΐ����Ƃ�Ƃ́�
���ӂɂ����Ƃ���ΐ����Ƃ���ΐ����u����Ď̂Ă�v���Ƃł͂Ȃ� �ΐ����l���邱��=�ΐ���t���邱��  �����Ŏ��̌������g�� ��������� (1)���g����x�����ɖ߂��� |
|
��2.�}�ɂ������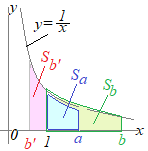
�܂�Cx=1�̉E���ɂ���ʐς� ���̂Ƃ��C 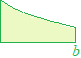 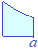
…(*1)
�v����ɁC
�������Cx=1�̉E���ɂ���ʐς𐳂Ƃ��C�}��b'�̂悤��x=1�̍����ɂ���ʐς͕��̕����������̂Ƃ��܂��D�i�ȏ�̂��Ƃ͐��w�V�ŏK���܂��j 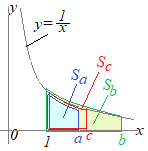 ���ɁC(1)���̕���ƕ��q�����ꂼ��c�܂ł̖ʐ�
���ɁC(1)���̕���ƕ��q�����ꂼ��c�܂ł̖ʐ� 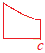  
…(*2)
(*2)�� |