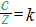|
=== �ǎ҂��z�F��ύX�������ꍇ ===
�������藝���O���̐F��ς���ɂ́C���̐F���N���b�N
�i�͂��߂Ɂj �@�O�p�`��\���Ƃ�
��
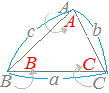 �����̏ꍇ�A���_�̖��O��A , B , C�̏��ɍ����ɕt���܂��B �����̏ꍇ�A���_�̖��O��A , B , C�̏��ɍ����ɕt���܂��B���ӂ̖��O�́u�����������p�v�̏������ŕ\���܂��B���������āAA�̑Ε�BC��a�Ƃ��܂��B���l�ɂ��āA���ɒf�菑�����Ȃ����b=AC , c=AB�ɂȂ�܂��B �����_�̖��OA , B , C�ł��̓��p��A�A��B�A��C�̑傫����\���A�P��sinA , sinB , sinC�ȂǂƏ����܂��B 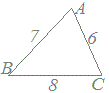 �y��z �y��z�E�}�ɂ�����a=BC=8, b=AC=6 , c=AB=7�ɂȂ�܂��B 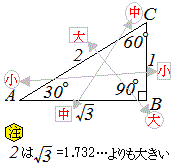 �i�p�x���傫���ƕӂ��傫���j �i�p�x���傫���ƕӂ��傫���j
�@�E�}�̂悤�ȎO�p�`��`���Ă݂�ƁA3�̊p�x�̒���B����ԑ傫���Ƃ��A���̑Ε�b��3�ӂ̒��ň�ԑ傫���Ȃ�܂��BA����ԏ������Ƃ��A���̑Ε�a��3�ӂ̒��ň�ԏ������Ȃ�܂��B�i���Ԃ̊p�xC�ɂ͒��Ԃ̕�c���Ή����܂��B�j
�@�������A 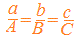 �̂悤�ȒP���ȊW�ɂ͂Ȃ�܂���B �̂悤�ȒP���ȊW�ɂ͂Ȃ�܂���B�ӂ̒������p�x�ɔ�Ⴗ�� 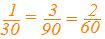 �̂ł͂Ȃ��A �̂ł͂Ȃ��A�@���́u�ӂ̒����͊p�x�̐����ɔ�Ⴗ���v  �Ƃ����W�ɂȂ��Ă��܂��B �Ƃ����W�ɂȂ��Ă��܂��B�@�����ŁA�ȉ��ɏq�ׂ�W���́u�����藝�v�ƌĂ�܂��B 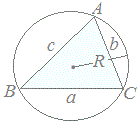 �y�����藝�z �y�����藝�z�@��ABC�̊O�ډ~�̔��a��R�Ƃ���Ƃ��A 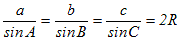
�y��z
���̐}�ɂ����āA 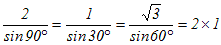 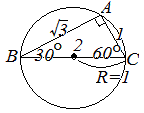 |
���̃y�[�W�̃}�C�i�[�`�F���W����J�o�[�Ńy�[�W
�i�O�[�O���u���K�[�Łj�́C�������
�y�����藝�𗝉����邽�߂ɑO��ƂȂ鎖���z
��1 �@�u�����v�Ƃ͎O�p���̂�����sin���̒l�̂��ƂŁA�����藝���g�����߂ɂ�0���`180���̎O�p���̒l�������Ȃ���Ȃ�܂���B �@���ۂɁA���ňËL���Č����Ȃ���Ȃ�Ȃ͎̂���9�̒l�����ł��B
��2�@��������sinA�͕ӂ̒����̔�Ƃ͌���Ȃ�!!
�Ⴂ����ǂ�ł�������Ȃ��l�ց�
�@���������C���̐}�C�̂悤�ȏꍇsinA�� 4/6 �ɂ͂Ȃ�܂���D 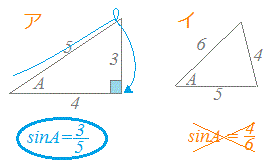 �@�O�p�`�́u2�ӂ̒����̔�v�������̒l�ɂȂ�̂͒��p�O�p�`�̏ꍇ�����ŁA����ȊO�̏ꍇ�ɂ�sinA�̒l�́u2�ӂ̒����̔�v�ɂ͂Ȃ�܂���B
�@�O�p�`�́u2�ӂ̒����̔�v�������̒l�ɂȂ�̂͒��p�O�p�`�̏ꍇ�����ŁA����ȊO�̏ꍇ�ɂ�sinA�̒l�́u2�ӂ̒����̔�v�ɂ͂Ȃ�܂���B�@�i�E�}�C�̂悤�ȏꍇ���܂߂āj��ʂɁA�p�xA�̒l�ɂ����sinA�̒l�����܂�A����Ƃ͕ʂɕӂ̒��������߂��Ă����ƍl���邱�Ƃ��d�v�ł��B
��3
�@���̂悤�ȁu��Ꭾ�v�̕ό`�Ɋ���邱�Ƃ��d�v�ł��B (1)�@���̊W���ɒ����ɂ́A2�̍l����������܂����A3�ȏ�̂Ƃ��ɂ��g����̂́A�ԍ����ɑΉ���������@�ł��B
�y��z
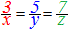
(2)�@�A�Ȃ��Ă����Ꭾ�́A�藣���Ďg���܂��B
A)�@�Q�ɕ����Ďg���܂��F 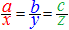 �� �� 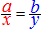 �� �� 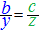
�y��z
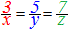 �� �� 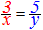 �� �� 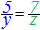
B)�@�u�t�������ڊǗ�����v
�y��z
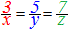 �� 3=kx , 5=ky , 7=kz �� 3=kx , 5=ky , 7=kz |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
�y�����藝�̏ؖ��z
��3(2)B)�́u�t�������ڊǗ�����v�Q��
�i�A�j�@A=90���̂Ƃ�
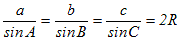 �̑���� �̑����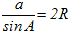 �A �A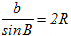 �A �A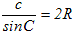 �ɕ����ďؖ����܂��B �ɕ����ďؖ����܂��B
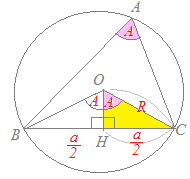
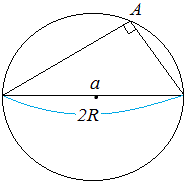
�E�}1�̂悤�ɁAA�͒��a�̏�ɗ��~���p�ɂȂ邩��A
�i�C�j�@0��<A<90���̂Ƃ�
sinA=sin90��=1�Aa=2R
���̂Ƃ��A
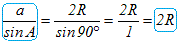
�i�A�j�ł��܂��ؖ��ł����̂́A���a�𗘗p��������ł����B�����ŁA���a�𗘗p������܂�������������Ȃ��ƍl���܂��B
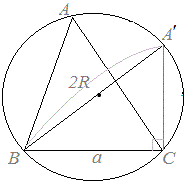
�@�E�}2�̂悤��B���璆�S��ʂ钼���������ƁABA’�͒��a�ɂȂ�܂��B���̂Ƃ��A
�i�E�j�@90��<A<180���̂Ƃ�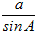 �́u���̒l�v�Ȃ̂ŁA�`���ς���Ă�a�̒l��sinA�̒l�������Ȃ�A�l�͓��������Ƃɒ��ӂ��܂��B �́u���̒l�v�Ȃ̂ŁA�`���ς���Ă�a�̒l��sinA�̒l�������Ȃ�A�l�͓��������Ƃɒ��ӂ��܂��B�@��������ƁA�E�}�̂悤��A��A’�Ƃ��~���p�Ƃ��ē������ꍇ�ɂ́A 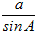 �� ��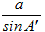 �ɓ������̂ŁA �ɓ������̂ŁA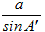 �����߂Ă��悢���ƂɂȂ�܂��B �����߂Ă��悢���ƂɂȂ�܂��B�@��A’BC�͒��p�O�p�`�ł�����A 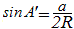 ���������� 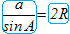
�i�C�j�ł��܂��ؖ��ł����̂́A���a�𗘗p��������ł����B�����ŁA������x���a�𗘗p���邱�Ƃ��l���܂��B�i���̉��̂ǂ��傤��_���܂��B�������A���x��90��<A<180���Ȃ̂ʼn~�̒��S�͎O�p�`�̊O�ɂ���܂����A���܂킸BO����������BA’�����܂��B�j
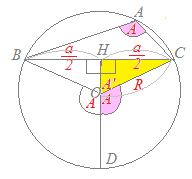
�@�E�}3�̂悤��B���璆�S��ʂ钼���������ƁABA’�͒��a�ɂȂ�܂��B���̂Ƃ��A
�ȏ�́i�A�j�i�C�j�i�E�j�ɂ��A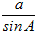 �́u���̒l�v�Ȃ̂ŁA�`���ς���Ă�a�̒l��sinA�̒l�������Ȃ�A�l�͓��������Ƃɒ��ӂ��܂��B �́u���̒l�v�Ȃ̂ŁA�`���ς���Ă�a�̒l��sinA�̒l�������Ȃ�A�l�͓��������Ƃɒ��ӂ��܂��B�@��������ƁA�E�}3�̂悤��A��A’�Ƃ��~�ɓ��ڂ���l�p�`�̌����������p�ɂȂ��Ă���Ƃ��́AA’=180��−A�ɂȂ�܂��̂ŁA��1�����Ă�������悤��sinA=sinA’�����藧���܂��B 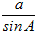 �� ��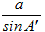 �ɓ������̂ŁA �ɓ������̂ŁA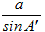 �����߂Ă��悢���ƂɂȂ�܂��B �����߂Ă��悢���ƂɂȂ�܂��B�@��A’BC�͒��p�O�p�`�ł�����A 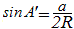 ���������� 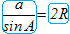 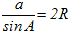 �������ꂽ���ƂɂȂ�܂��B �������ꂽ���ƂɂȂ�܂��B���l�ɂ���B�AC�ɂ��Ă��ؖ����邱�Ƃ��ł��܂��̂ŁA 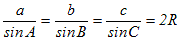 ���ؖ�����܂��B ���ؖ�����܂��B
|
�}1
  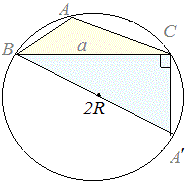
�y��1�z
�i�l�����j
�@��ABC�ɂ����āAa=8 , A=45��, B=60���̂Ƃ��Ab�����߂Ă��������B
��3(2)A)�̍l������
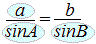 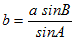 �Ɖ������Ƃ��ł��܂��B �Ɖ������Ƃ��ł��܂��B���i���������̘b�Ƃ��āj���̂悤�ȁu���Ձv�������āA�㉺�i�ӂƊp�j�P�g�Ƒ��̊p�i�܂��͕Ӂj���������Ă���A�c���1�́u�����藝�v�ʼn����܂��B�i�������A�����sin ��t���Ďg���܂��B�j
�i�j 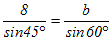 ��� 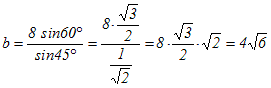 ����i���j ����i���j
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
�y��2�z
�i�l�����j
�@��ABC�ɂ����āAa=2 , 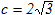 , A=30��, �̂Ƃ��AC�����߂Ă��������B , A=30��, �̂Ƃ��AC�����߂Ă��������B
���u���Ձv
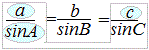 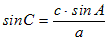 �Ɖ������Ƃ��ł��܂��B �Ɖ������Ƃ��ł��܂��B�i�������A�����藝�Łh�p�x�h�����߂�ƁA���̓��Ă̂悤�ɉ���2�o�Ă��邱�Ƃ�����܂��B���̂Ƃ��A2�Ƃ����ł��邱�Ƃ��A1���������ő����͉��łȂ����Ƃ�����܂��BA+C>180���̂悤�ȂƂ��́A���̉��͕s�K���ł��B�j 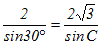 ���A 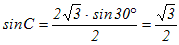 C=60�� , 120������i���j
A=30�� , C=60�� , 120���̂�����̑g�ł��AB=90�� , 30���ƂȂ��ĎO�p�`�͂ł��܂��̂ŁA�����Ƃ����ł��B
|
�y��3�z
�i�l�����j
�@��ABC�ɂ����āAa=3 , A=120��, �̂Ƃ��A�O�ډ~�̔��aR�����߂Ă��������B
���u�t�������ڊǗ����܂��v
�@ 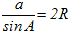 �����̂܂g���܂��B �����̂܂g���܂��B
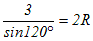 ���A 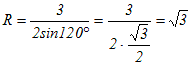 ����i���j ����i���j
|
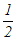
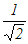
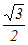
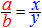 �� 3�ȏ�ɂ͎g���Ȃ�
�� 3�ȏ�ɂ͎g���Ȃ�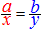 �� ��
�� ��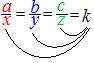
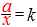 ��
�� 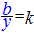 ��
��