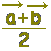== 位置ベクトルの応用 ==
■[要点]
(1)2点 ,\hspace{5}B(\vec{b})) \( A(\vec{a}),\hspace{5px}B(\vec{b}) \) \( A(\vec{a}),\hspace{5px}B(\vec{b}) \)を結ぶベクトルは,
 \( \overrightarrow{\rm{AB}}=\vec{b}-\vec{a} \) \( \overrightarrow{\rm{AB}}=\vec{b}-\vec{a} \)
\(\vec{a}-\vec{b}\) ではなく、
\(\vec{b}-\vec{a}\) である点に注意
※ (終点) − (始点) の形が重要
(記号についての注意)
高校の数学では,点 Aの座標が &chco=aa2200) \( (3,\hspace{5px}4) \) \( (3,\hspace{5px}4) \)であるとき, &chco=0000ff) \( \textcolor{blue}{A(3,\hspace{5px}4)} \) \( \textcolor{blue}{A(3,\hspace{5px}4)} \)と書き, &chco=ff0000) \( \textcolor{red}{A=(3,\hspace{5px}4)} \) \( \textcolor{red}{A=(3,\hspace{5px}4)} \)とは書かないのと同様に,点 Aの位置ベクトルが  \( \vec{a} \) \( \vec{a} \)であるとき, &chco=0000ff) \( \textcolor{blue}{A(\vec{a})} \) \( \textcolor{blue}{A(\vec{a})} \)と書き,  \( \textcolor{red}{A=\vec{a}} \) \( \textcolor{red}{A=\vec{a}} \)とは書きません.
大学の数学と違って,点の関数などを考えないので,点が点以外の何かに等しいという記号を使う必要がありません.
「 A,その位置ベクトルは  \( \vec{a} \) \( \vec{a} \)」という感じに棒読みに受け取るとよい.
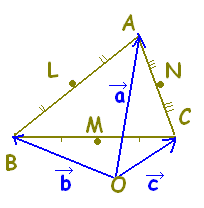
 \( \overrightarrow{\rm{OA}}=\vec{a},\hspace{5px}\overrightarrow{\rm{OB}}=\vec{b} \) \( \overrightarrow{\rm{OA}}=\vec{a},\hspace{5px}\overrightarrow{\rm{OB}}=\vec{b} \)
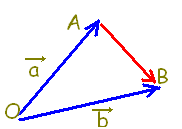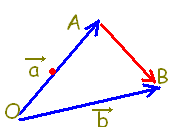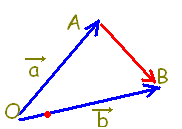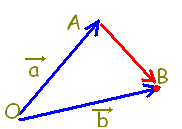
だから
 \( \overrightarrow{\rm{AB}}=\overrightarrow{\rm{AO}}+\overrightarrow{\rm{OB}} \) \( \overrightarrow{\rm{AB}}=\overrightarrow{\rm{AO}}+\overrightarrow{\rm{OB}} \)
 \( =-\overrightarrow{\rm{OA}}+\overrightarrow{\rm{OB}} \) \( =-\overrightarrow{\rm{OA}}+\overrightarrow{\rm{OB}} \)
 \( =-\vec{a}+\vec{b} \) \( =-\vec{a}+\vec{b} \)
 \( =\vec{b}-\vec{a} \) \( =\vec{b}-\vec{a} \)
[考え方のポイント]
分かっている道(青の道)をつないで,
分からない道(赤の道)の別ルートを作る!
|
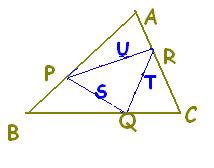
(2)2点 ,\hspace{5}B(\vec{b})) \( A(\vec{a}),\hspace{5px}B(\vec{b}) \) \( A(\vec{a}),\hspace{5px}B(\vec{b}) \)を結ぶ線分 ABを m:nに内分する点 Pの位置ベクトル  \( \vec{p} \) \( \vec{p} \)は,
 \( \displaystyle \vec{p}=\frac{n\vec{a}+ m\vec{b}}{m+ n} \) \( \displaystyle \vec{p}=\frac{n\vec{a}+ m\vec{b}}{m+ n} \)
特に, ,\hspace{5}B(\vec{b})) \( A(\vec{a}),\hspace{5px}B(\vec{b}) \) \( A(\vec{a}),\hspace{5px}B(\vec{b}) \)の中点 Mの位置ベクトル  \( \vec{m} \) \( \vec{m} \)は,
 \( \displaystyle \vec{m}=\frac{\vec{a}+\vec{b}}{2} \) \( \displaystyle \vec{m}=\frac{\vec{a}+\vec{b}}{2} \)
■解説■
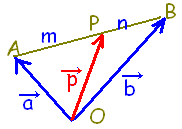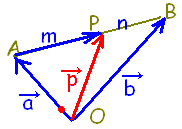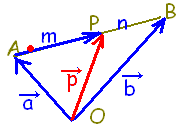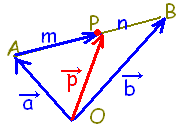
求めているのは Pの位置ベクトルなので,  \( \overrightarrow{\rm{AP}} \) \( \overrightarrow{\rm{AP}} \)ではなくて  \( \overrightarrow{\rm{OP}} \) \( \overrightarrow{\rm{OP}} \)であることに注意
(直線 ABの中に入っているものではなく,原点 Oから Pに向かっているものが位置ベクトル)
まず  \( \overrightarrow{\rm{AB}}=\vec{b}-\vec{a} \) \( \overrightarrow{\rm{AB}}=\vec{b}-\vec{a} \)
次に,この  \( \overrightarrow{\rm{AB}} \) \( \overrightarrow{\rm{AB}} \)
を  \( \dfrac{m}{m+ n} \) \( \dfrac{m}{m+ n} \)
倍に縮めると
) \( \displaystyle \overrightarrow{\rm{AP}}=\frac{m}{m+n}(\vec{b}-\vec{a}) \) \( \displaystyle \overrightarrow{\rm{AP}}=\frac{m}{m+n}(\vec{b}-\vec{a}) \)
できたベクトルを  \( \displaystyle \overrightarrow{\rm{OA}} \) \( \displaystyle \overrightarrow{\rm{OA}} \)につぎ足すと
) \( \displaystyle \overrightarrow{\rm{OA}}+\overrightarrow{\rm{AP}}=\vec{a}+\frac{m}{m+n}(\vec{b}-\vec{a}) \) \( \displaystyle \overrightarrow{\rm{OA}}+\overrightarrow{\rm{AP}}=\vec{a}+\frac{m}{m+n}(\vec{b}-\vec{a}) \)
}{m%2B n}) \( \displaystyle \overrightarrow{\rm{OP}}=\frac{m\vec{a}+n\vec{a}+m(\vec{b}-\vec{a})}{m+ n} \) \( \displaystyle \overrightarrow{\rm{OP}}=\frac{m\vec{a}+n\vec{a}+m(\vec{b}-\vec{a})}{m+ n} \)
 \( \displaystyle =\frac{n\vec{a}+m\vec{b}}{m+ n} \) \( \displaystyle =\frac{n\vec{a}+m\vec{b}}{m+ n} \)
※結果としてできた公式を見てみると,
ABを m:nに内分するとき,  \( \vec{a} \) \( \vec{a} \)には図形的に遠い方の比率 nを掛けています.  \( \vec{b} \) \( \vec{b} \)には図形的に遠い方の比率 mを掛けています.
(「いじわる公式」「へそ曲げ公式」と覚えておくと間違わない)
|