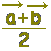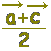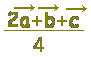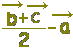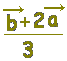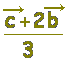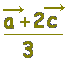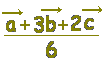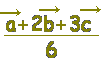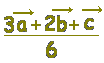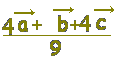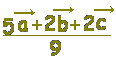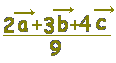 【問題1】
△ABC
【問題1】
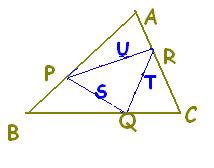
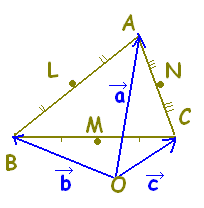
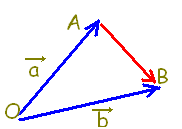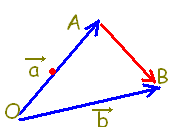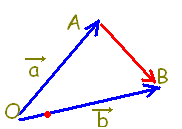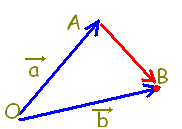
△ABCの頂点 A, B, Cの位置ベクトルを  \( \vec{a},\hspace{5px}\vec{b},\hspace{5px}\vec{c} \) \( \vec{a},\hspace{5px}\vec{b},\hspace{5px}\vec{c} \)
とし, AB, BC, CAの中点を L, M, Nとするとき,次のベクトルを  \( \vec{a},\hspace{5px}\vec{b},\hspace{5px}\vec{c} \) \( \vec{a},\hspace{5px}\vec{b},\hspace{5px}\vec{c} \)を用いて表しなさい。
○初めに問題を選び,続いて選択肢を選びなさい。合っていれば消えます。
○[解説]を読む場合でも読まない場合でも,新たに問題を選択すれば,解答を再開できます.
≪問題≫
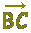

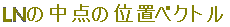


≪選択肢≫
 解説
解説
 \( \overrightarrow{\rm{BC}}=\overrightarrow{\rm{BO}}+\overrightarrow{\rm{OC}}=-\vec{b}+\vec{c} \) \( \overrightarrow{\rm{BC}}=\overrightarrow{\rm{BO}}+\overrightarrow{\rm{OC}}=-\vec{b}+\vec{c} \)
 \( \overrightarrow{\rm{AB}}=\overrightarrow{\rm{AO}}+\overrightarrow{\rm{OB}}=-\vec{a}+\vec{b} \) \( \overrightarrow{\rm{AB}}=\overrightarrow{\rm{AO}}+\overrightarrow{\rm{OB}}=-\vec{a}+\vec{b} \)
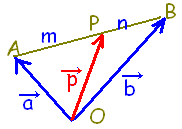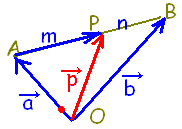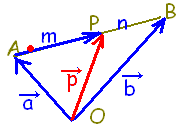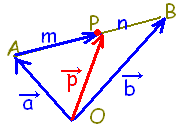
 \( \overrightarrow{\rm{OL}}=\dfrac{\vec{a}+\vec{b}}{2} \)
Lの位置ベクトルは \( \overrightarrow{\rm{OL}}=\dfrac{\vec{a}+\vec{b}}{2} \)
Lの位置ベクトルは \( \overrightarrow{\rm{OL}}=\dfrac{\vec{a}+\vec{b}}{2} \),Nの位置ベクトルは \( \overrightarrow{\rm{OL}}=\dfrac{\vec{a}+\vec{b}}{2} \),Nの位置ベクトルは \( \overrightarrow{\rm{ON}}=\dfrac{\vec{a}+\vec{c}}{2} \),したがって,LNの中点の位置ベクトルは \( \overrightarrow{\rm{ON}}=\dfrac{\vec{a}+\vec{c}}{2} \),したがって,LNの中点の位置ベクトルは \( \displaystyle \frac{\dfrac{\vec{a}+ \vec{b}}{2}+ \dfrac{\vec{a}+ \vec{c}}{2} }{2}=\frac{2\vec{a}+\vec{b}+\vec{c}}{4} \) \( \displaystyle \frac{\dfrac{\vec{a}+ \vec{b}}{2}+ \dfrac{\vec{a}+ \vec{c}}{2} }{2}=\frac{2\vec{a}+\vec{b}+\vec{c}}{4} \)
 \( \displaystyle \overrightarrow{\rm{AM}}=\overrightarrow{\rm{AO}}+\overrightarrow{\rm{OM}}=-\vec{a}+\frac{\vec{b}+\vec{c}}{2} \)
Lの位置ベクトルは \( \displaystyle \overrightarrow{\rm{AM}}=\overrightarrow{\rm{AO}}+\overrightarrow{\rm{OM}}=-\vec{a}+\frac{\vec{b}+\vec{c}}{2} \)
Lの位置ベクトルは \( \displaystyle \overrightarrow{\rm{OL}}=\frac{\vec{a}+\vec{b}}{2} \),Nの位置ベクトルは \( \displaystyle \overrightarrow{\rm{OL}}=\frac{\vec{a}+\vec{b}}{2} \),Nの位置ベクトルは \( \displaystyle \overrightarrow{\rm{ON}}=\frac{\vec{a}+\vec{c}}{2} \),したがって, \( \displaystyle \overrightarrow{\rm{ON}}=\frac{\vec{a}+\vec{c}}{2} \),したがって, \( \displaystyle \overrightarrow{\rm{LN}}=-\frac{\vec{a}+\vec{b}}{2}+ \frac{\vec{a}+\vec{c}}{2}=\frac{\vec{c}-\vec{b}}{2} \) \( \displaystyle \overrightarrow{\rm{LN}}=-\frac{\vec{a}+\vec{b}}{2}+ \frac{\vec{a}+\vec{c}}{2}=\frac{\vec{c}-\vec{b}}{2} \)
|
 【問題1】
【問題1】