← PC�p�͕ʕ�
|
�����Z���w�U�̎O�p���ɂ��āC���̃T�C�g�ɂ͎��̋��ނ�����܂��D
//-->
Google��YAHOO ! �Ȃǂ��猟���ł��̕łɒ��ڗ��Ă��܂����̂őO��W���悭������Ȃ��Ƃ����ꍇ�́C���̕ł��Ɍ��Ă��������D�@ �����ݒn�ł��D 
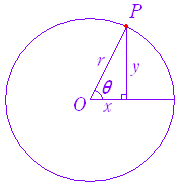
 ���̊p�E���̊p ���̊p�E���̊p
 ��ʊp ��ʊp
 �O�p���̒�` �O�p���̒�`

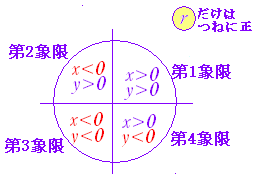
 ��Q�ی��̊p ��Q�ی��̊p
 ��R�ی��̊p ��R�ی��̊p
 ��S�ی��̊p ��S�ی��̊p

 �O�p���̐����i�܂Ƃ߁j �O�p���̐����i�܂Ƃ߁j

 �ʓx�@�̒P�ʃ��W�A�� �ʓx�@�̒P�ʃ��W�A��
 �ʓx�@�F�O�p���̒l �ʓx�@�F�O�p���̒l

 sin(��+��)�Ȃ� sin(��+��)�Ȃ�
 y=sin(��−��)�̃O���t y=sin(��−��)�̃O���t

 y=a sin b(x−p)+q �̃O���t y=a sin b(x−p)+q �̃O���t

 y=a cos b(x−p)+q �̃O���t y=a cos b(x−p)+q �̃O���t

 �U���ƃO���t �U���ƃO���t
 �����ƃO���t �����ƃO���t
 �O�p������ �O�p������
 �O�p�s���� �O�p�s����
 ��(2) ��(2)
  ���@�藝�A�{�p�����A�R�{�p�����A���p���� ���@�藝�A�{�p�����A�R�{�p�����A���p����

 ���@�藝�i���K���j ���@�藝�i���K���j
 ��(2) ��(2)

 �{�p�E���p�����i���K���j �{�p�E���p�����i���K���j
 �Ϙa�E�a�ς̌��� �Ϙa�E�a�ς̌���
 ��(2) ��(2)
 ��(3) ��(3)
 �O�p���̍������� �O�p���̍�������
|
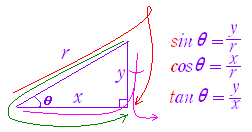
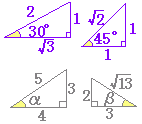
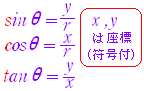
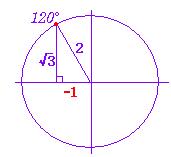 �@�Ⴆ�C
�@�Ⴆ�C