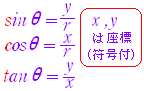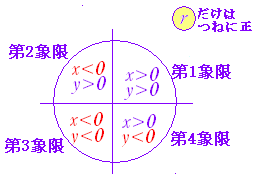
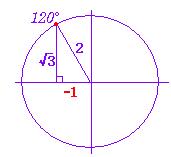
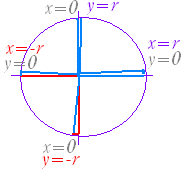
三角関数の値（定義 I）

■　解説

===　数学Ｉにおける三角比の定義（復習）===

○　三角比の定義
　数学Ｉにおいて三角比は，図1のような直角三角形の辺の長さの比で定義された．この定義は，直角三角形が描けることを前提としている．

例　図2の直角三角形について

　sin 30°=

　cos 45°=

　tanα=

　sinβ=

　負の角度や90°以上の角度では，このような直角三角形が描けないので，定義を変える．その場合，右の定義の全部を捨てるのでなく，「式はそのまま使い」「x , y の意味だけを変える」．(↓)

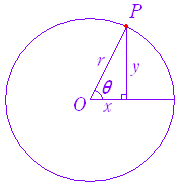
図１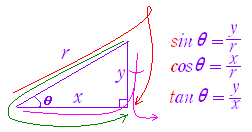

覚え方：
sinθは筆記体でs の字を書く，cosθはcを書く，tanθはt を書く．
(cosθだけは角度θから出発せずに，θに回り込む．)
図2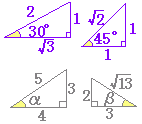

===　数学II における三角関数の定義 ===

○　三角関数の定義

　原点を中心とする半径 r の円周上を点Pが動くとき，動径OPがx軸の正の向きとなす角をθとする．
　このとき，点Pの座標を ( x, y ) ，円の半径を r として，三角関数を

で定義する．

○　三角関数の符号
　右図のように各象限ごとに x , y の符号が決まっているので，三角関数の符号が定まる．

符号	sinθ	cosθ	tanθ
第1象限	+	+	+
第2象限	+	−	−
第3象限	−	−	+
第4象限	−	+	−

例
　第2象限では，x<0 , y>0　（r はつねに正）　だから　
　sinθ=>0

　cosθ=<0

　tanθ=<0

　例えば，
　sin 120°=

　cos 120°= −

　tan 120°= −

例

※　180°，0°のライン（赤道線）から30°，45°，60°などの図を書いて考えるとよい．

　なお，座標軸上での三角関数の値は，次のとおり

sin 0°=0，　cos 0°= 1，tan 0°= 0

sin 90°= 1，　cos 90°= 0 ，tan 90°は定義されない

sin 180°=0 ，　cos 180°= − 1，tan 180°=0

sin 270°= − 1，　cos 270°= 0 ，tan 270°は定義されない