== 三角方程式 ==
【三角方程式とは】
•  \( \sin\theta=\dfrac{1}{2} \) \( \sin\theta=\dfrac{1}{2} \)や  \( \cos\theta=-\dfrac{\sqrt{2}}{2} \) \( \cos\theta=-\dfrac{\sqrt{2}}{2} \)のように角度が未知数になっている方程式を三角方程式という.
• 三角方程式は,次の例題のように単位円を利用して解くと分かりやすい.
【例題1】
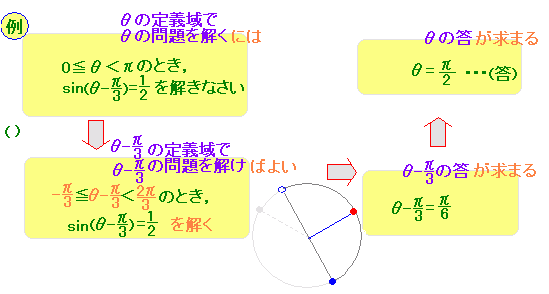
 \( 0\leqq \theta\leqq \pi \) \( 0\leqq \theta\leqq \pi \)のとき,  \( \sin\theta=\dfrac{1}{2} \) \( \sin\theta=\dfrac{1}{2} \)を満たす θの値を求めてください.
サインはy
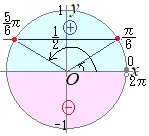
 \( \sin\theta=\dfrac{y}{r} \) \( \sin\theta=\dfrac{y}{r} \)だから,単位円(半径rが1の円)を描くと,  \( \sin\theta=y \) \( \sin\theta=y \)になる
⇒「サインはy」と覚えておく
(解答)
右図の単位円で,y座標が \( \dfrac{1}{2} \)となる角度は, \( \dfrac{1}{2} \)となる角度は, \( \theta=\dfrac{\pi}{6} \)と \( \theta=\dfrac{\pi}{6} \)と \( \theta=\dfrac{5\pi}{6} \)…(答) \( \theta=\dfrac{5\pi}{6} \)…(答)
#超初心者のビックリ答案#
何十年も高校で教えていると,ビックリ答案に出会うことがある.馬鹿にしているのでなく,危険な落とし穴として注意しておこう!
 \( \sin\theta=\dfrac{1}{2} \) \( \sin\theta=\dfrac{1}{2} \)から  \( \theta=\dfrac{1}{2\sin} \) \( \theta=\dfrac{1}{2\sin} \)と答えた生徒がいた.
 \( \sin\theta \) \( \sin\theta \)は  \( \sin \) \( \sin \)と  \( \theta \) \( \theta \)のかけ算ではないのだ!  \( \sin \) \( \sin \)などというものはないのだ.
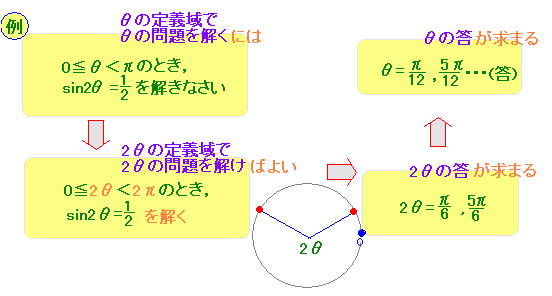
#この問題はなぜ解けるのか#
本当のことを言えば,この問題が解けるのは,
 \( \sin\dfrac{\pi}{6}=\dfrac{1}{2} \) \( \sin\dfrac{\pi}{6}=\dfrac{1}{2} \)と  \( \sin\dfrac{5\pi}{6}=\dfrac{1}{2} \) \( \sin\dfrac{5\pi}{6}=\dfrac{1}{2} \)という答えを覚えているから解けるのです.もっとはっきり言えば,「筆算で解ける」のは,次の表に出てくる  \( \theta,\hspace{3px}y \) \( \theta,\hspace{3px}y \)の組み合わせだけです.
| θ | 0 |  \( \dfrac{\pi}{6} \) \( \dfrac{\pi}{6} \) |  \( \dfrac{\pi}{4} \) \( \dfrac{\pi}{4} \) |  \( \dfrac{\pi}{3} \) \( \dfrac{\pi}{3} \) |  \( \dfrac{\pi}{2} \) \( \dfrac{\pi}{2} \) |  \( \dfrac{2\pi}{3} \) \( \dfrac{2\pi}{3} \) |  \( \dfrac{3\pi}{4} \) \( \dfrac{3\pi}{4} \) |  \( \dfrac{5\pi}{6} \) \( \dfrac{5\pi}{6} \) | π |
| y | 0 |  \( \dfrac{1}{2} \) \( \dfrac{1}{2} \) |  \( \dfrac{1}{\sqrt{2}} \) \( \dfrac{1}{\sqrt{2}} \) |  \( \dfrac{\sqrt{3}}{2} \) \( \dfrac{\sqrt{3}}{2} \) | 1 |  \( \dfrac{\sqrt{3}}{2} \) \( \dfrac{\sqrt{3}}{2} \) |  \( \dfrac{1}{\sqrt{2}} \) \( \dfrac{1}{\sqrt{2}} \) |  \( \dfrac{1}{2} \) \( \dfrac{1}{2} \) | 0 |
この表にない値,例えば  \( \sin\theta=\dfrac{1}{5},\hspace{3px}\dfrac{1}{4},\hspace{3px}\dfrac{1}{3},\hspace{3px}\dfrac{2}{3},\hspace{3px}\dfrac{3}{4},\hspace{3px}\cdots \) \( \sin\theta=\dfrac{1}{5},\hspace{3px}\dfrac{1}{4},\hspace{3px}\dfrac{1}{3},\hspace{3px}\dfrac{2}{3},\hspace{3px}\dfrac{3}{4},\hspace{3px}\cdots \)のどれも「筆算では」解けません.解けるのは,この表にある  \( \sin\theta=0,\hspace{3px}\dfrac{1}{2},\hspace{3px}\dfrac{1}{\sqrt{2}},\hspace{3px}\dfrac{\sqrt{3}}{2},\hspace{3px}1 \) \( \sin\theta=0,\hspace{3px}\dfrac{1}{2},\hspace{3px}\dfrac{1}{\sqrt{2}},\hspace{3px}\dfrac{\sqrt{3}}{2},\hspace{3px}1 \)の場合だけです.
中学校で習う1次方程式の解き方  \( 3x=2\rightarrow x=\dfrac{2}{3} \) \( 3x=2\rightarrow x=\dfrac{2}{3} \)など違って, ) \( \sin\theta=a\hspace{5px}(0\leqq a\leqq 1) \) \( \sin\theta=a\hspace{5px}(0\leqq a\leqq 1) \)を「数式変形で」解く方法はありません.  \( \sin\theta=\dfrac{1}{3} \) \( \sin\theta=\dfrac{1}{3} \)のような問題は「教科書の巻末に付いている三角関数表を見て」解くのです.
| θ | … | 19° | 20° | 21° | … |
| 正弦 | … | 0.3256 | 0.3420 | 0.3584 | … |
θ=約19°
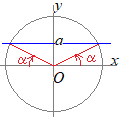
これに対して,定期試験や入学試験などで三角関数表が付いていない場合には,上に述べた表に出てくる問題しか出ないことになります(符号が逆のものは出ます).
|




 (A)
(A) 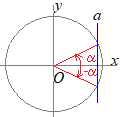 (A)
(A) 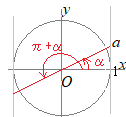 (A)
(A)