|
【1.極座標の定義】 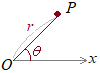 平面上の点Pの位置を極O(xy平面の原点にあたる)からの距離rと始線OXとOPがなす角度θ(偏角という)で表したものを極座標といいます.
平面上の点Pの位置を極O(xy平面の原点にあたる)からの距離rと始線OXとOPがなす角度θ(偏角という)で表したものを極座標といいます.点Pの極座標はP(r, θ)の形で書きます. 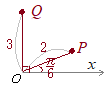 【例】
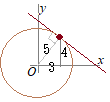
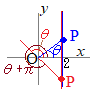
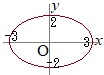
【例】右図の各点の極座標は です. 角度θを1回転すると同じ位置に来るので,θ+2nπで表される点は同じ場所になります. 必要に応じて,0≦θ<2πの範囲に制限する場合や,制限なしで使う場合もあります. また,rは通常r≧0を使いますが,負の値も使いたい場合は,偏角にπを加えたものを考えます.
【例】
|
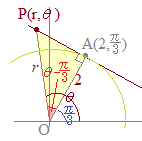
【2.極座標と直交座標との関係】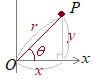 右図より,次の関係があります.
右図より,次の関係があります.(r, θ)→(x, y)
x=rcosθ
(x, y)→(r, θ)y=rsinθ θは 【3.極方程式の例】 極方程式は,平面上の図形をr, θの関係式として表すものです.
【例1】
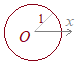 中心が極Oにあって,半径が1の円の方程式は
中心が極Oにあって,半径が1の円の方程式はr=1 (方程式に書かれていない変数θは任意の角をとり得るものと解釈されます.したがって0≦θ<2πの1回転するすべての点を表すから,円になります.) 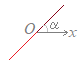 【例2】
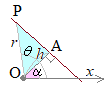
【例2】偏角がαの直線の方程式は θ=α (方程式に書かれていない変数rは任意の角をとり得るものと解釈されます. r≧0に制限すれば半直線になりますが,r<0のときθ=α+πとすると,右図の赤で示した部分も含まれ,直線になります.) |
 点
点
 ■ 極座標で考えれば ■
■ 極座標で考えれば ■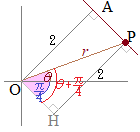 ■ 極座標で考えれば ■
■ 極座標で考えれば ■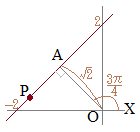 【例題1】を参考にすると,このグラフは,(極座標で表した)点
【例題1】を参考にすると,このグラフは,(極座標で表した)点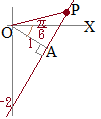 【例題1】を参考にすると,このグラフは,(極座標で表した)点
【例題1】を参考にすると,このグラフは,(極座標で表した)点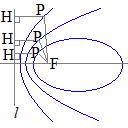
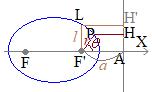
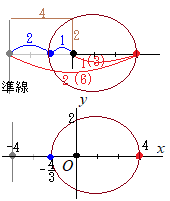
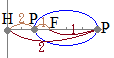 このように楕円(
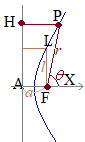
このように楕円(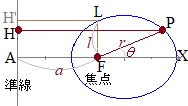 焦点から始線に垂直な直線を引き,曲線との交点を
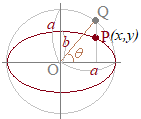
焦点から始線に垂直な直線を引き,曲線との交点を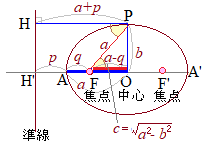 右図のような楕円
右図のような楕円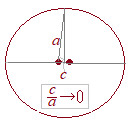
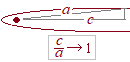
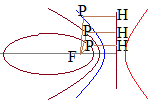
 [B] 双曲線の図では
[B] 双曲線の図では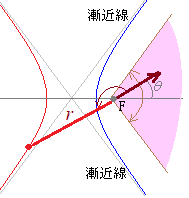
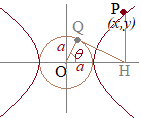
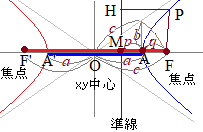 右図のような双曲線
右図のような双曲線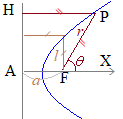
 (楕円の場合,右側の)焦点
(楕円の場合,右側の)焦点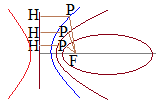
 離心率は
離心率は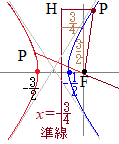 公式のまま読み取るためには,分母の定数項が1になっていなければなりませんので,次のように変形します.
公式のまま読み取るためには,分母の定数項が1になっていなければなりませんので,次のように変形します.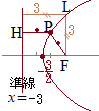 離心率は
離心率は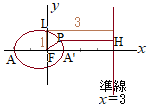 公式のまま読み取るためには,分母の定数項が1になっていなければなりませんので,次のように変形します.
公式のまま読み取るためには,分母の定数項が1になっていなければなりませんので,次のように変形します.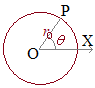 [1] 極
[1] 極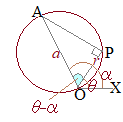 [2] 極
[2] 極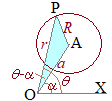 [3] 点
[3] 点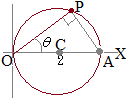 始線上に(極座標で)点
始線上に(極座標で)点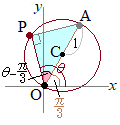 (極座標で)点
(極座標で)点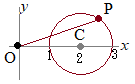 上記の公式[3]において
上記の公式[3]において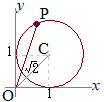 xy直交座標のままでグラフを考えると,点
xy直交座標のままでグラフを考えると,点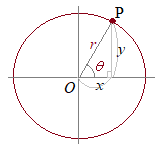
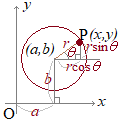
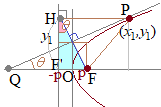
 xy直交座標に直すと
xy直交座標に直すと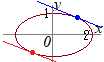 条件式から変数を代入しようとしても,このままの形では代入できないので
条件式から変数を代入しようとしても,このままの形では代入できないので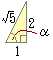 ただし,角
ただし,角