|
■接線の方程式 ■1 接線の方程式
《要点》
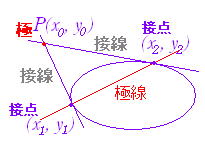
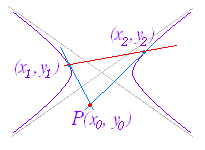
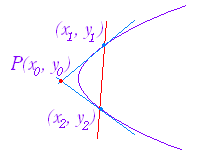
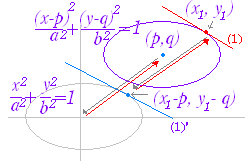
【解説】■1 (1) 楕円 +=1 上の点 P(x1 , y1) における接線の方程式は +=1 …(1) (2) 双曲線 −=1 上の点 P(x1 , y1) における接線の方程式は −=1 …(2) (3) 放物線 y2=4px 上の点 P(x1 , y1) における接線の方程式は y1 y=2p(x+x1 ) …(3)
《なんとなく規則性》
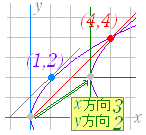
元の方程式 x2 → 接線では積にする x1x 元の方程式 2x → 接線では和にする x+x1 (1) +=1 の両辺を x で微分すると +=0 より =− となるから 接線の傾きは − 接点 P(x1 , y1) における接線の方程式は y−y1=−(x−x1) a2y1y−a2y12=−b2x1x+b2x12 a2y1y+b2x1x=b2x12+a2y12 +=+ ここで,接点 P(x1 , y1) は楕円上の点だから +=1 を満たす.よって, +=1 → (1) (2) −=1 の両辺を x で微分すると −=0 より = となるから 接線の傾きは 接点 P(x1 , y1) における接線の方程式は y−y1=(x−x1) a2y1y−a2y12=b2x1x−b2x12 b2x1x−a2y1y=b2x12−a2y12 −=− ここで,接点 P(x1 , y1) は双曲線上の点だから −=1 を満たす.よって, −=1 → (2) (続く→)
|
 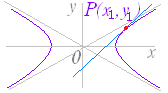 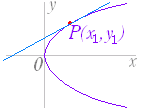
【復習:陰関数の微分法(数学 III)】 曲線の方程式が 例えば,(A)において導関数を求めるには,そのまま両辺を x で微分するとよい.その際,y の関数 y2 を x で微分するためには,合成関数微分法を用いる: = これにより, (y2)=(y2)=2y (A)の両辺を x で微分すると 2ax+2by =0 となり, = − が求まる.(このような場合,導関数は x も y も用いて表わす.) (→続き) (3) y2=4px の両辺を x で微分すると 2y =4p より = となるから 接線の傾きは 接点 P(x1 , y1) における接線の方程式は y−y1=(x−x1) y1y−y12=2px−2px1 y1y=2px+y12−2px1 ここで,接点 P(x1 , y1) は放物線上の点だから y12=4px1 を満たす.よって, y1y=2px+2px1=2p(x+x1) → (3) |
| 《基本事項のチェック》 (1) 楕円 +=1 上の点 P(1, ) における接線の方程式は +=1 x+2y=4 (2) 双曲線 −=1 上の点 P(, ) における接線の方程式は −=1 2x−3y=18 |
(3) 放物線 y2=4x 上の点 P(1 ,−2) における接線の方程式は
−2y=2(x+1) x+y+1=0 |
| 問題 |
→閉じる←
(1) −=1 より x−4y=16 (2) x−y=1 より 3x−y=3 (3) −6y=6(x+3) より x+y+3=0 |