|
■点Aの周りの回転
【複素数の極形式】
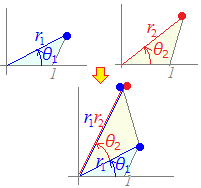
【例1】2つの複素数を極形式で表したとき,それらの積は回転・拡大を表す. すなわち
z1=r1(cosθ1+i sinθ1)
特に,絶対値が1の複素数を掛けると,原点の周りに回転したものを表す.z2=r2(cosθ2+i sinθ2) のとき z1z2=r1r2{ cos(θ1+θ2)+i sin(θ1+θ2) }となるから z1z2はz1をr2倍して,角θ2だけ回転したものを表す. z1z2はz2をr1倍して,角θ1だけ回転したものを表すと考えてもよい.
z1=r1(cosθ1+i sinθ1)
z2=cosθ2+i sinθ2 のとき z1z2=r1{ cos(θ1+θ2)+i sin(θ1+θ2) }となる.
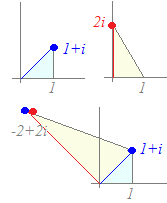
z1=1+i=(cos+i sin)
【例2】z2=2i=2(cos+i sin) のとき z1z2=2i(1+i)=−2+2i=2{ cos+i sin } となるから z1z2はz1を2倍して,角だけ回転したものを表す.
z1=1+i=2(cos+i sin)
z2=i=cos+i sin のとき z1z2=i(1+i)=−+i=2{ cos+i sin } となるから z1z2はz1を,角だけ回転したものを表す. |
図1
  |
|
【点αの周りの回転】
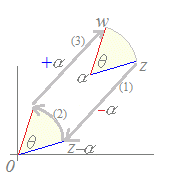
(解説)点zを点αの周りに角θだけ回転した点wは w=(z−α)(cosθ+i sinθ)+α (1) 初めに,点αと点zをいずれも−αだけ平行移動すると,点αは原点に,点zは点z−αにきます. (2) 次に,z−αを原点の周りに角θだけ回転すると (z−α)(cosθ+i sinθ)
になります.(3) 最後に,この点を+αだけ平行移動すると,回転した点が得られます. w=(z−α)(cosθ+i sinθ)+α
【例3】
点z=3を点α=1の周りにθ=だけ回転して得られる点wは
w=(3−1)(cos+i sin)+1
=2(+i)+1=1+i+1=2+i
|
図3
  |
|
【三角形の形状】
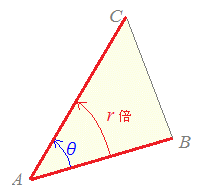
A(z1 ), B(z2 ), C(z3 )について z3−z1=(z2−z1)×r(cosθ+i sinθ)…(1) もしくは =r(cosθ+i sinθ)…(2) のとき AC=AB×r ∠BAC=θ
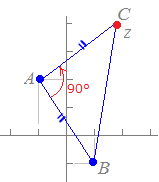
【例4】
(解答)複素数平面上に3点A, B, Cが反時計回りの順に並んでいる.A(−1+2i), B(1−i), C(z)とするとき,△ABCが∠A=90°の直角二等辺三角形となるようにzを定めてください. Aの周りにABを90°だけ回転したときACに重なるから, z−(−1+2i)={ 1−i−(−1+2i) }×(cos90°+i sin90°) ={ 1−i+1−2i) }×i=(2−3i)×i=3+2i z=3+2i−1+2i=2+4i…(答)
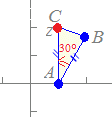
【例5】
(解答)複素数平面上に3点A, B, Cが反時計回りの順に並んでいる.A(1), B(2+i), C(z)とするとき,△ABCが∠A=30°, AB=ACの二等辺三角形となるようにzを定めてください. Aの周りにABを30°だけ回転したときACに重なるから, z−1=(2+i−1)×(cos30°+i sin30°) =(1+i)×=2i z=1+2i…(答) |
図4
   |
| 【問題】各々正しいものを選んでください. |
 (+i−2i)(cos30°+i sin30°)+2i
(+i−2i)(cos30°+i sin30°)+2i=(−i)+2i=2+2i |
 (0−3−i)(cos90°+i sin90°)+3+i
(0−3−i)(cos90°+i sin90°)+3+i=(−3−i)i+3+i=−3i+1+3+i=4−2i |
|
|
(3)複素数平面上に3点A, B, Cが反時計回りの順に並んでいる.A(−1+2i), B(3+i), C(z)とするとき,△ABCがABを斜辺とする直角二等辺三角形となるようにzを定めてください.
HELP |
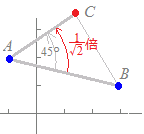 ACはABを45°回転して,倍したものだから
ACはABを45°回転して,倍したものだからz−(−1+2i) =(4−i)(cos45°+i sin45°) =(4−i)= z=+(−1+2i)= |
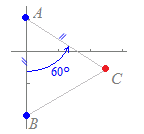 ACはABを60°回転したものだから
ACはABを60°回転したものだからz−i =(−3i)(cos60°+i sin60°) =(−3i)= z=+i= |
|
|
(5)複素数平面上で3点A(z1 ), B(z2 ), C(z3 )について,z3−z1=(z2−z1)(1+i)が成り立つとき,△ABCはどのような形の三角形ですか.
HELP ∠A=90°の直角二等辺三角形 ∠B=90°の直角二等辺三角形 ∠C=90°の直角二等辺三角形 正三角形 |
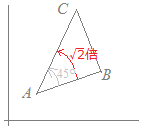 1+i=(cos45°+i sin45°)だから
1+i=(cos45°+i sin45°)だからAC=AB× ∠CAB=45° したがって, ∠B=90°の直角二等辺三角形 (別解) だからBA⊥BC, BA=BC ゆえに,∠B=90°の直角二等辺三角形 |