陰関数の導関数

← PC用は別頁

*** 数学Ⅱ（多項式まで） ***

不定形の極限

微分係数

増減表

*** 高卒から大学初年度程度 ***

■陰関数の導関数
■ｙ＝ｘ²+3ｘのように，ｙがｘの関数として解かれた形で表されているものを陽関数表示といいます。
■ｘ²+ｙ²＝4のように，ｙがｘの関数として明示的に解かれておらず，ｘ，ｙの関係式が与えられているものを陰関数表示といいます。

■陰関数で表示されているときは，

「両辺をそのままｘで微分」
→を含む式を作る
→について解く

という手順で導関数を求めることができます。このとき，導関数は，ｙを含んだ式になるのが普通です。
■例１

■例２

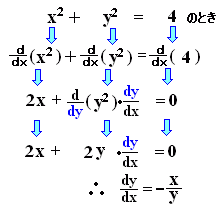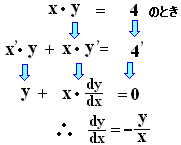■陰関数で表示されているときは，１つのｘの値に対してｙがただ1つ定まるとは限らず，ｙ’もただ１つとは限りません。
例　ｘ²+ｙ²＝4のとき，ｘ＝1→ｙは２つ，ｙ’も２つ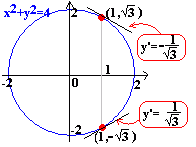

導関数の表示にｙも用いて

のように表すことができます。

例　ｘｙ＝4のとき、ｘ＝2→ｙは１つ，ｙ’も１つ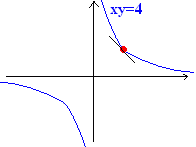

この場合のように，陽にも解ける関数を陰のまま微分してもかまいません：（

　は　

　と一致します。）

※以下の問題で，
「正答の場合に表示される図」⇒

「誤答の場合に表示される図」⇒

----------------
※解答すれば，解説が読めます．解答しなければ，解説は出ません．

［問題］　次の関係式から

を求めなさい。
（正しいものを選択肢から選びなさい。）

１

［選択肢］

解説
両辺をxで微分する
$\frac{d}{dx}(\frac{x^2}{9})-\frac{d}{dx}(\frac{y^2}{4})=\frac{d}{dx}(1)$
第２項は，xの関数になっておらずyの関数になっているのでdyで割って掛ける
$\frac{2}{9}x-\frac{dy}{dx}\frac{d}{dy}(\frac{y^2}{4})=0$
$\frac{2}{9}x-\frac{dy}{dx}\frac{2y}{4}=0$
$\frac{dy}{dx}=\frac{2x}{9}\times \frac{4}{2y}=\frac{4x}{9y}$

２ xy=3

解説
両辺をxで微分する
$\frac{d}{dx}(xy)=\frac{d}{dx}(3)$
左辺の微分は積の微分法を使う
$\frac{d}{dx}(x)y+ x\frac{d}{dx}(y)=\frac{d}{dx}(3)$
$y+ x\frac{dy}{dx}=0$
$\frac{dy}{dx}=-\frac{y}{x}$

３ x³+y³-3xy=0

解説
両辺をxで微分する
$\frac{d}{dx}(x^3)+ \frac{d}{dx}(y^3)-\frac{d}{dx}(3xy)=\frac{d}{dx}(0)$
第２項は，xの関数になっておらずyの関数になっているのでdyで割って掛ける．また，第３項は積の微分法を使う．
$3x^2+ \frac{dy}{dx}\frac{d}{dy}(y^3)-3\Bigl(\frac{d}{dx}(x)y+ x\frac{d}{dx}(y)\Bigr)=0$
$3x^2+ \frac{dy}{dx}\times 3y^2-3\Bigl(y+ x\frac{dy}{dy}\Bigr)=0$
$(3y^2-3x)\frac{dy}{dx}=3y-3x^2$
$\frac{dy}{dx}=\frac{3y-3x^2}{3y^2-3x}=\frac{y-x^2}{y^2-x}=\frac{x^2-y}{x-y^2}$

４ cosy=sinx

$\frac{dy}{dx}=\tan x$ $\frac{dy}{dx}=\cot x$

$\frac{dy}{dx}=\frac{\sin y}{\cos x}$ $\frac{dy}{dx}=-\frac{\cos x}{\sin y}$
解説
両辺をxで微分する
$\frac{d}{dx}(\cos y)=\frac{d}{dx}(\sin x)$
左辺は，xの関数になっておらずyの関数になっているのでdyで割って掛ける．
$\frac{dy}{dx}\frac{d}{dy}(\cos y)=\frac{d}{dx}(\sin x)$
$\frac{dy}{dx}(-\sin y)=\cos x$
$\frac{dy}{dx}=-\frac{\cos x}{\sin y}$

■［個別の頁からの質問に対する回答］[陰関数の導関数について／17.8.7］

問３の解説の2行目の式で、yの微分になってしまっているところがあります。
問題3の解説の二行目-3(d/dy(x)y + x d/dy(y))は-3(d/dx(x)y + x d/dx(y)) では？・解説の中で出てきた答えが選択肢の中にないのはなぜ？どれが正しいのかがわからず混乱しています。改善よろしくお願いします。
＝＞［作者］：連絡ありがとう．前半について，訂正しました．
後半について，そのような質問はあり得ないと考えていますが，一応確認のために加筆しました．（一勝一敗になる）
$\frac{x^2-y}{y^2-x}=\frac{y-x^2}{x-y^2}$
は，自明の理なので解説は不要だと思いますが．

［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．

...（携帯版）メニューに戻る

...（PC版）メニューに戻る