← PC用は別頁
*** 高卒から大学初年度程度 ***
逆三角関数の微分法 マクローリン展開 偏微分

== 導関数の符号の求め方 ==
■解説
※この頁で扱うのは１つの完結した問題ではなく，次の手順の内で赤で示した部分に絞った練習です．
元の関数yが与えられる
→y’を求める
→y’の符号を決める
→yの増減を矢印で表す
【例１】
y=2x3+3x2−12x+1のとき
y’=6x2+6x−12=6(x+2)(x−1) …(A)
となるので，このy’の符号をxの値に応じて定めることにより，次のような増減表を作ることができます．
x…−2…1…
y’+0−0+
y極大極小
　この頁では上の手順のうちで赤で示した部分に絞って，y’の符号を求める練習を行います．
以下において元の関数yや増減表の中でのyの矢印は省略します．

≪考え方１≫
y’の式からy’の符号を求めるために
y’のグラフを描く方法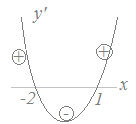
　上の式(A)ではy’の最高次の項の係数が正（6）なので，y’のグラフは右図のようになります．
（このグラフはyのグラフではなくy’のグラフである点に注意．yのグラフはこの図とは異なります．）
　このグラフにより，y’の符号は
+| 0 |−| 0 |+
のように定まります．


≪考え方２≫
y’の式から直接y’の符号を求める方法
　上の式(A)ではy’の最高次の項の係数が正（6）なのでxが十分大きな値のとき，y’=6(x+2)(x−1)のすべての因数が正になります．
6は正
x+2は正（x+2はx=−2のとき0，xがそれより大きければ正になります．）
x−1は正（x−1はx=1のとき0，xがそれより大きければ正になります．）
　そこで，右側から順に符号を埋めて行き，0となる所で符号が変わるようにするとy’の符号が定まります．
※もし，y’=6(x+2)(x−1)2のようにx−1の因数が二重解の形になっているときは，x=1の所で２回変わると考えます．
※もし，y’=6(x+2)2(x−1)のようにx+2の因数が二重解の形になっているときは，x=−2の所で２回変わると考えます．
※もし，y’=6(x+2)3(x−1)のようにx+2の因数が三重解の形になっているときは，x=−2の所で３回変わると考えます．

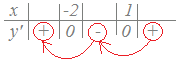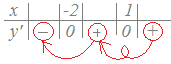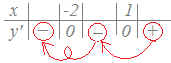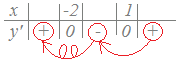【例２】
y’=−2(x+2)(x−1)(x−3)のとき …(B)
≪考え方１≫
y’の式からy’の符号を求めるために
y’のグラフを描く方法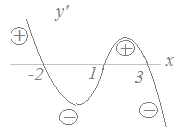
　式(B)ではy’の最高次の項の係数が負（−2）なので，y’のグラフは右図のようになります．
（このグラフはyのグラフではなくy’のグラフである点に注意．yのグラフはこの図とは異なります．）
　このグラフにより，y’の符号は
+| 0 |−| 0 |+| 0 |−
のように定まります．


≪考え方２≫
y’の式から直接y’の符号を求める方法
　式(B)ではy’の最高次の項の係数が負（−2）なのでxが十分大きな値のとき，y’=−2(x+2)(x−1)(x−3)の因数のうち−2だけが負で他はすべて正になります．
−2は負
x+2は正（x+2はx=−2のとき0，xがそれより大きければ正になります．）
x−1は正（x−1はx=1のとき0，xがそれより大きければ正になります．）
x−3は正（x−3はx=3のとき0，xがそれより大きければ正になります．）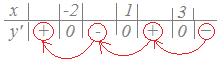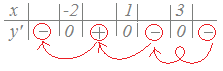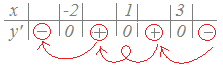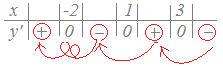
　そこで，右側から順に符号を埋めて行き，0となる所で符号が変わるようにするとy’の符号が定まります．
※もし，y’=−2(x+2)(x−1)(x−3)2のようにx−3の因数が二重解の形になっているときは，x=3の所で２回変わると考えます．
※もし，y’=−2(x+2)(x−1)2(x−3)のようにx−1の因数が二重解の形になっているときは，x=1の所で２回変わると考えます．
※もし，y’=−2(x+2)3(x−1)(x−3)のようにx+2の因数が三重解の形になっているときは，x=−2の所で３回変わると考えます．




（まとめ）


■問題[第1問 / 全10問]
1＿ 2＿ 3＿ 4＿ 5＿ 6＿ 7＿ 8＿ 9＿ 10＿ 11＿ 12＿ 13＿ 14＿
ある関数の導関数y’が次の式になるとき，増減表のy’の符号を定めてください．（＋－のどちらか一方を選んでください．）
次の参考図はyのグラフではなく，y’のグラフであることに注意
また，y’軸方向のスケールは，必要に応じて拡大縮小されています．
5 −5

...（携帯版）メニューに戻る

...メニューに戻る