← PC用は別頁
|
■三角関数 y=sinx,y=cosx,y=tanx などを微分するためには,次の極限値を求めておかなければなりません。 1■ この極限値が重要となる理由に分けて説明します。 1■この極限値が重要となる理由  |
|
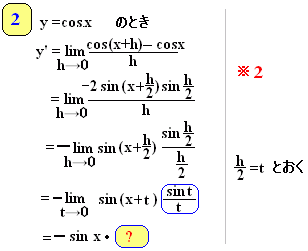 ⇒ y=tanxの微分はsinx,cosxの結果を用いて商の微分法で求められます。
※1
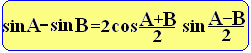
※2 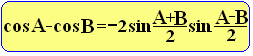
|
| 2■ この極限値
次のグラフは 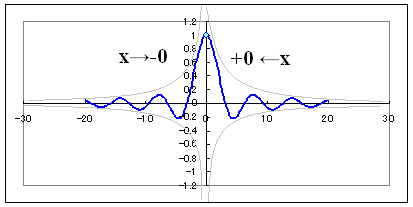 ・x=0のとき分母が0となるため関数値 f(0) は存在しませんが極限値は f(x)→1(x→0)となっています。 ■教科書では,もう少していねいに,次のように図を用いて証明するのが普通です。 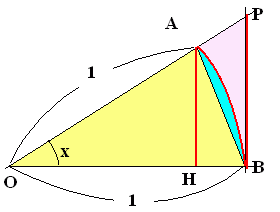
図1において
[重要な極限値(1)]
※
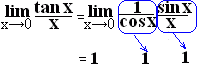
※ |
|
[例題]
[答案例] sin4x を 変形するのは難しそうですが,4xで「割って、掛ける」ことは簡単です。 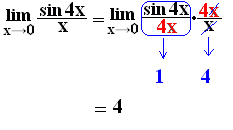
[例題]
[答案例] 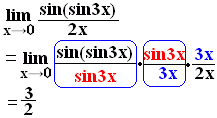 |
  |
|
次の極限値を求めなさい。
○初めに問題を選び,次に選択肢を選びなさい。正しければ消えます。
[問題]
○分からないとき,問題を選んでから解答するまでにヒントボタンを押せばヒントが出ます。 |
[選択肢]
 |
 |
|
[注]直前にPC版から入られた場合は,自動転送でスマホ版に来ていますので,ブラウザの[戻るキー]では戻れません(堂々巡りになる).下記のリンクを使ってメニューに戻ってください.
|
|
■[個別の頁からの質問に対する回答][重要な極限値(1)について/18.8.13]
ありがとう
■[個別の頁からの質問に対する回答][重要な極限値について/16.11.14]
=>[作者]:連絡ありがとう. 大学の授業が全然理解できなかったので調べてこのページに来ました。
読むだけ読んで、わかった気になって、実際はわかっていないということが多いため、
問題を解いて理解できたか確かめられる機能とても良いと思いました。
=>[作者]:連絡ありがとう. |