[解説]
位置ベクトルの表す点Pは,
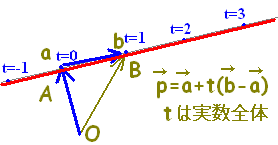
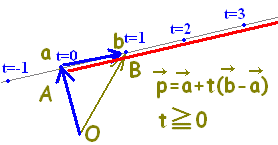
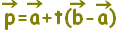 ( t は実数全体)には,直線AB全体が対応します。・・・(1)
( t は実数全体)には,直線AB全体が対応します。・・・(1)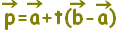 ( t≧0)には,半直線ABが対応します。・・・(2)
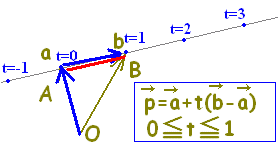
( t≧0)には,半直線ABが対応します。・・・(2)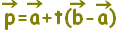 ( 0≦t≦1)には,線分ABが対応します。・・・(3)
( 0≦t≦1)には,線分ABが対応します。・・・(3)
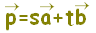 (s+t=1)には,直線AB全体が対応します。・・・(4)
(s+t=1)には,直線AB全体が対応します。・・・(4)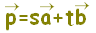 (s+t=1, t≧0)には,半直線ABが対応します。・・・(5)
(s+t=1, t≧0)には,半直線ABが対応します。・・・(5)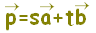 (s+t=1, t≧0, s≧0)には,線分ABが対応します。・・・(6)
(s+t=1, t≧0, s≧0)には,線分ABが対応します。・・・(6)
=(1-t) = (4)・・・→(1)
|
 |
●次の2つの図を比較して,「ひらめくもの」があれば,イメージとして大切にしましょう。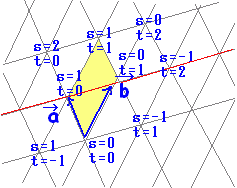 ←→ ←→ 通常のxy平面に対応する図 ←→ 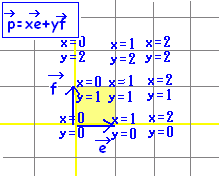 |
s+tが1でないとき
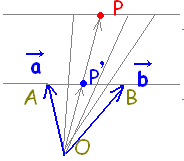
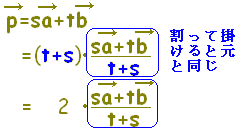 のように変形すると,□(右図のP’)はABの内分点(s,t>0のとき),又は外分点(s,tの一方が負の数のとき)だから,OPはOP’を2倍にしたもの。 のように変形すると,□(右図のP’)はABの内分点(s,t>0のとき),又は外分点(s,tの一方が負の数のとき)だから,OPはOP’を2倍にしたもの。 |
 |
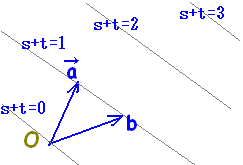
| s+t の値に応じて,点Pは右図のような直線上に存在する。 |
 |
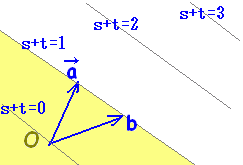
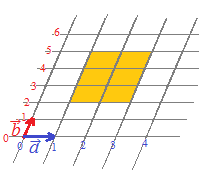
となる点Pの存在する範囲は右図(黄色の部分) |
 |
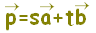 (s+t≦1, t≧0, s≧0)には,△OABの内部および周上が対応します。・・・(7)
(s+t≦1, t≧0, s≧0)には,△OABの内部および周上が対応します。・・・(7)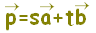 (s+t≦1/2, t≧0, s≧0)には,右の三角形の内部および周上が対応します。・・・(8)
(s+t≦1/2, t≧0, s≧0)には,右の三角形の内部および周上が対応します。・・・(8)
 質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,
質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,