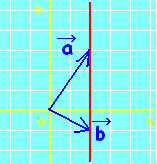
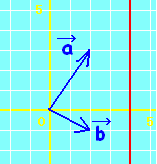
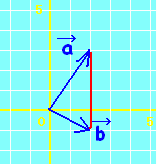
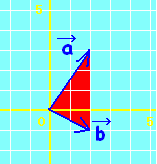
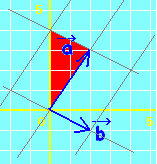
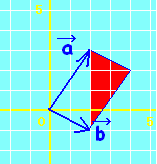
 位置ベクトルの表す点Pは, には,直線AB全体が対応します。・・・(1) 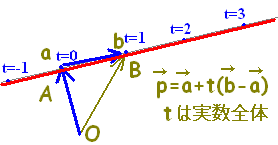 には,半直線ABが対応します。・・・(2) 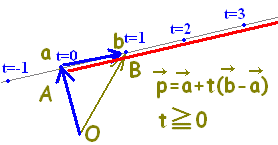 には,線分ABが対応します。・・・(3) 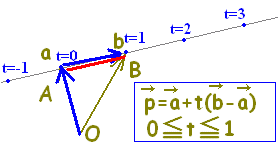 |
|
←→ ←→ はs=1−tを使ってsを消去すると と同じだから はs=1−tを使ってsを消去すると と同じだから からs=1−tを使ってsを消去する.  ※sを消去するときは,生き残ったtがsに付着していた条件を引き継いでやらなければならないことに注意
※sを消去するときは,生き残ったtがsに付着していた条件を引き継いでやらなければならないことに注意
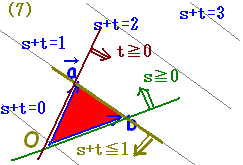
s+t=1, s≧0, t≧0 ←→s=1−t, s≧0, t≧0 ←→s=1−t, 1−t≧0, t≧0 ←→0≦t≦1, (s=1−t) となるから と同じ |
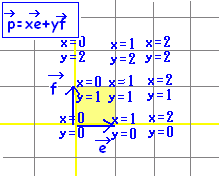
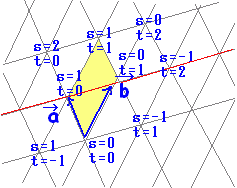 (参考2)
(参考2)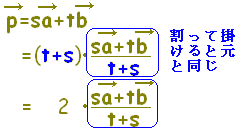
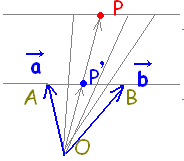
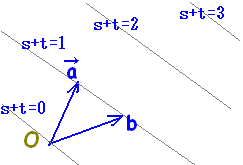
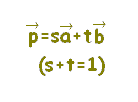
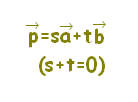
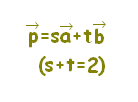
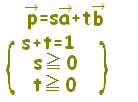
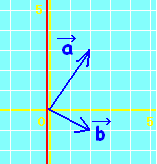
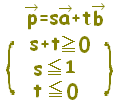
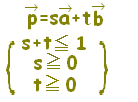
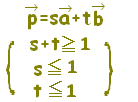
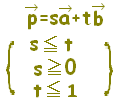
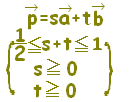
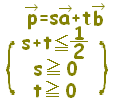
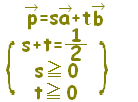
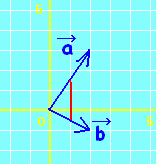
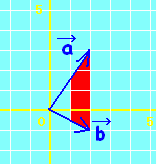
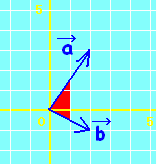

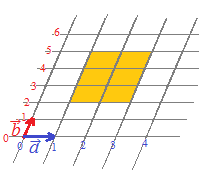 質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,
質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,