同一直線上にあるための条件

■３点が同一直線上にあるための条件

「３点が同一直線上にあるための条件」のことを「共線条件」ということがあります：線を共にするということ。

[解説]
　ベクトルの実数倍の応用として，３点が同一直線上にあるための条件をベクトルで表現する方法があります。
　図のように，「始点をＡにそろえておけば」２つのベクトルの一方を伸縮して他方になれば，３点は一直線上にあります。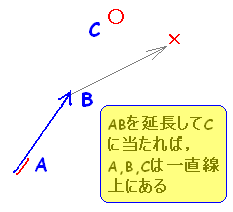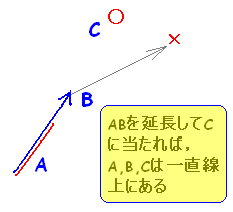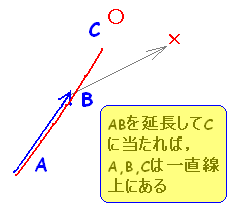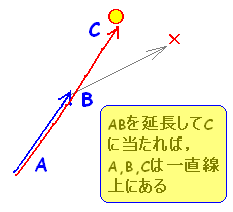

【要点】３点Ａ，Ｂ，Ｃが一直線上にある　
←→　 $\vec{AC}=t\vec{AB}$ (となる実数ｔが存在する)

※「ＣＢ，ＣＡの組」，「ＢＡ，ＢＣの組」，「ＡＢ，ＣＢ組」でも出来ますが，上のイメージ図で「伸ばせば当たる」形にするのがコツ。　

【例１】
　 $\vec{OP}=2\vec{a}+ 3\vec{b},\hspace{5}\vec{OQ}=3\vec{a}-4\vec{b},\hspace{5}\vec{OR}=\vec{a}+ 10\vec{b}$ のとき３点P, Q, Rは一直線上にあることを証明しなさい。

答案例
$\vec{PQ}=(3\vec{a}-4\vec{b})-(2\vec{a}+ 3\vec{b})$

（※終点−始点の形が2点を結ぶベクトル）

$=\vec{a}-7\vec{b}$
$\vec{PR}=(\vec{a}+ 10\vec{b})-(2\vec{a}+ 3\vec{b})$

（※終点−始点の形が2点を結ぶベクトル）

$=-\vec{a}+ 7\vec{b}$
だから
$\vec{PR}=(-1)\vec{PQ}$ が成り立つ．
ゆえに，３点P, Q, Rは一直線上にある。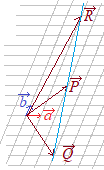

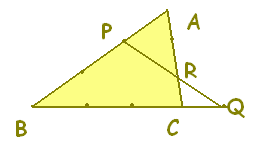
※この問題では，ベクトル $\vec{a},\hspace{5}\vec{b}$ の形が具体的に示されていないことに注意．
すなわち，ベクトル $\vec{a},\hspace{5}\vec{b}$ がどんな形であっても成り立つ．
右図の網目において，平行四辺形の形がどのように歪んでも，P, Q, Rは一直線上にある。

【問1】 $\vec{OP}=\vec{a}+ 7\vec{b},\hspace{5}\vec{OQ}=5\vec{a}+ 4\vec{b},\hspace{5}\vec{OR}=9\vec{a}+ \vec{b}$ のとき３点P, Q, Rは一直線上にあることを証明しなさい．

答案

$\vec{PQ}=\vec{OQ}-\vec{OP}=(5\vec{a}+ 4\vec{b})-(\vec{a}+ 7\vec{b})$
$=4\vec{a}-3\vec{b}$
$\vec{PR}=\vec{OR}-\vec{OP}=(9\vec{a}+ \vec{b})-(\vec{a}+ 7\vec{b})$
$=8\vec{a}-6\vec{b}$
だから
$\vec{PR}=2\vec{PQ}$

→閉じる←

【問2】
$\vec{OP}=\frac{\vec{a}-\vec{b}}{6},\hspace{5}\vec{OQ}=\frac{\vec{a}+\vec{b}}{2},\hspace{5}\vec{OR}=\frac{5\vec{a}+ 4\vec{b}}{12}$ のとき３点P,Q,Rは一直線上にあることを証明しなさい。

答案

$\vec{PQ}=\vec{OQ}-\vec{OP}=\frac{\vec{a}+ \vec{b}}{2}-\frac{\vec{a}-\vec{b}}{6}$
$=\frac{2\vec{a}+ 4\vec{b}}{6}=\frac{\vec{a}+ 2\vec{b}}{3}$
$\vec{PR}=\vec{OR}-\vec{OP}=\frac{5\vec{a}+ 4\vec{b}}{12}-\frac{\vec{a}-\vec{b}}{6}$
$=\frac{3\vec{a}+ 6\vec{b}}{12}=\frac{\vec{a}+ 2\vec{b}}{4}$
だから
$\vec{PR}=\frac{3}{4}\vec{PQ}$

→閉じる←

【問3】
３点A(3, 2), B(6, 1), C(x, 4)が同一直線上にあるようにxの値を定めなさい。

答案

$x=-3$

→閉じる←

【問4】
△ＡＢＣにおいて辺ＡＢを１：２に内分する点をＰ，辺ＢＣを４：１に外分する点をＱ，辺ＣＡを１：２に内分する点をＲとすると，３点Ｐ，Ｑ，Ｒは同一直線上にあることを示しなさい。

答案

$\vec{PQ}=2\vec{PR}$

→閉じる←

〇==メニューに戻る

■［個別の頁からの質問に対する回答］[３点が同一直線上にあるための条件について／17.5.10］

解答ページを作って欲しい
＝＞［作者］：連絡ありがとう．なるほど解答が分からない場合がありますので，解答を付けます．ただしその頁内に付けます．

■［個別の頁からの質問に対する回答］[３点が同一直線上にあるための条件について／17.2.6］

3点が一直線上にあるようにxの値を求める問題で、学校の宿題で3点が(2,x),(x,0),(-2,6)というように二箇所にxが入っている問題が出たのですが、その場合は解き方はこの頁に載っていたものとは変わるのでしょうか？教えていただけると嬉しいです。
＝＞［作者］：連絡ありがとう．同じ考え方で解けます．なお，問題の写し間違いのせいか，このままでは解けません（虚数解になります．）
他に，直線の方程式で考える場合はこの頁（ただし，未知数をxのままで計算すると直線の方程式のxと混ざってしまうのでtに変えるなど工夫を要す）