|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
【2013年度センター試験.数学Ⅰ・数学A】第1問 [2]
三角形に関する条件p, q, rを次のように定める。
p : 三つの内角がすべて異なる
条件pの否定をpで表し,同様にq, rはそれぞれ条件q, rの否定を表すものとする。q : 直角三角形でない r : 45°の内角は一つもない (1) 命題「r ⇒ ( p または q )」の対偶は 「ク ⇒ r」である。 クに当てはまるものを,次の⓪~③のうちから一つ選べ。
⓪ ( p かつ q )
① (p かつ q)
② (p または q )
③ (p または q)
|
[解答を見る]
【逆・裏・対偶】
ⅰ) 元の命題 p ⇒ q に対して q ⇒ pを逆という p ⇒ qを裏という q ⇒ pを対偶という ⅱ) 元の命題とその対偶とは真偽が一致する.
【ド・モルガンの法則】
(1) 「r ⇒ ( p または q )」の対偶はⅰ) ( p かつ q )と( p または q )の真偽は一致する. ⅱ) ( p または q )と( p かつ q )の真偽は一致する. ( p または q ) ⇒ r すなわち pかつq ⇒ r だから,①→ク |
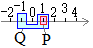 [集合図の包含関係で示す場合]
[集合図の包含関係で示す場合]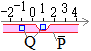 [集合図の包含関係で示す場合]
[集合図の包含関係で示す場合] [集合図の包含関係で示す場合]
[集合図の包含関係で示す場合] [集合図の包含関係で示す場合]
[集合図の包含関係で示す場合]