|
→ スマホ用は別頁
このページのバックアップ・ページ
(グーグルブロガー版)は,こちら⇒ |
この教材のレベルは,高等数学Ⅰの教科書のレベルです.応用的な内容を期待される方は,他のページを見てください.
数学Ⅰを初めて学ぶ人や長年の空白期間の後に復習したい人など,初歩から学び直す読者を想定しています. 1. 単項式
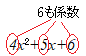
5x, −3x2のように,数や文字をいくつか掛け合わせて得られる式を単項式といい,数の部分を係数,掛け合わせてある文字の個数をその単項式の次数という.
【参考1.1】
係数は見たままの「物」に付けられた名前であるのに対して,次数は掛けられている文字の「個数」に付けられた名前となっていて,〇〇数と言っても同列の名前でないことに注意 【例】 単項式「3a」の係数は3, 次数は1  【例】 単項式「4x3」の係数は4, 次数は3  なお,次数はいくらかと尋ねられたとき,「次数は3」のように1つの数で答えるのが普通であるが,文章の中では「次数は3次」「3次式」という言い方もする. |
 レレレの零?簡単過ぎて難しい!!深堀すると更に難しくなるので,「聞いたことがある」程度にしておこう
レレレの零?簡単過ぎて難しい!!深堀すると更に難しくなるので,「聞いたことがある」程度にしておこう

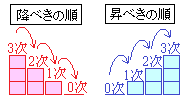 【参考3.2】
【参考3.2】