|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
��w�������Ƃ��Ă̓�Փx�i�M�҂̈�ہj ��@�{�F������
���@�ʁF������
����F������
|
|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
��w�������Ƃ��Ă̓�Փx�i�M�҂̈�ہj ��@�{�F������
���@�ʁF������
����F������
|
|
�y���1�z������
�m�����ǂށn�@i�������P�ʂƂ���D���̂Ƃ��C �i2021�N�x�k�C�w���� �H�w���j
|
|
�y���2�z������
�@���f�� �i2015�N�x���� �H�w���j
|
|
�m�����ǂށn
�h�E���A�u���̒藝�ɂ�� ���l�ɂ��āC�h�E���A�u���̒藝�ɂ��  �E�}�̎O�p�`�ɂ����āC�]���藝��p���ĕӂ̒���L��\��
�E�}�̎O�p�`�ɂ����āC�]���藝��p���ĕӂ̒���L��\�� |
|
�y���3�z������
�U�@���f�� (�A) 0�@(�J) 1�@(�T) 2�@(�^) 3�@(�i) 4�@(�n) 5�@(�}) 6�@(��) 7�@(��) 8�@(��) 9�@ �V �Ƃ���D (�A) 0�@(�J) 1�@(�T) 2�@(�^) 3�@(�i) 4�@(�n) 5�@(�}) 6�@(��) 7�@(��) 8�@(��) 9�@ �i2017�N�x������ȑ� ��w���j
|
|
�U �m�����ǂށn
�e�X�̕��f�����Ɍ`���ŕ\���� ���������āCZ�̐�Βl�� Z�̕Ίp�� Z2n�������ƂȂ������ 13n=6k�in (>0), k�͐����j 13, 6�݂͌��ɑf������ n=6t (>0) k=13t ����āC���R��n�̍ŏ��l��6→(�})����i���j |
|
�V �m�����ǂށn |
|
�y���4�z������
�@�Q�̕��f��α=i�C (1)�@z���Ɍ`���ŕ\���Ȃ����D (2)�@�ȉ����A�C�C�ɓ���l�����߂Ȃ����D �@z��α�����_�𒆐S�Ƃ����A������]���C���_����̋������C�{�������̂ł���D (3)�@zn�����̎����ƂȂ�ŏ��̎��R����n�Ƃ���D���̂Ƃ��Cn�����zn�̐�Βl�����߂Ȃ����D �i2017�N�x������ ���H�w�Q�j
|
|
�m�����ǂށn
(1) (2) 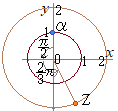 ���_�𒆐S�Ƃ��āC
���_�𒆐S�Ƃ��āC(3) ������C���ꂪ���̎����ƂȂ�ɂ� �@�����ŁC5, 6�݂͌��ɑf������ k=5t n�̍ŏ��l��6�C|zn|=64����i���j |
|
�y���5�z������
�@���f���Ɋւ��鎟�̖₢�ɓ�����D�������Ci�͋����P�ʂƂ���D (1)�@������z3=i��3�̉�z1, z2, z3�����߂�D�������C0��argz1<argz2<argz3<2π�Ƃ���D (2)�@���� (3)�@a�𐳂̎����Ƃ���D���f��z0��z03=ia���݂����C����z0�̕\���_��(2)�ŋ��߂��}�`��ɂ���Ƃ���D���̂Ƃ��Ca��z0�̒l�����ꂼ�ꋁ�߂�D �i2017�N�x�F�s�{�� �H�w���j
|
|
(1) �m�����ǂށn
z=r(cosθ+isinθ)�C�ir��0, 0��θ<2π�j�Ƃ��� �h�E���A�u���̒藝�ɂ�� z3=r3(cos3θ+isin3θ) �ƂȂ�. ���ꂪ�Ci�ɓ������Ȃ邱�Ƃ��� �@�@r=1���[1] �������C0��θ<2π����C0��3θ<6π�̏��������̂́Cn=0, 1, 2�̂Ƃ� �A�j n=0�̂Ƃ� �C�j n=1�̂Ƃ� �E�j n=2�̂Ƃ� �ȏォ�� |
|
(2) �m�����ǂށn �@����́C  �@���Ȃ킿�C���f��
�@���Ȃ킿�C���f��(3) z0�̕\���_��(2)�ŋ��߂��}�`��ɂ��邩��Cz0�̕Ίpθ�́C�iy�����܂ށj��3�ی��̊p�ŁC�E�}��P����Q�܂ł̊Ԃɂ���D ����� z03=ia (a>0)�ƂȂ�̂� �̂Ƃ��D���̂Ƃ� |
|
�y���6�z������
�m�����ǂށn�@a��b��ab<0�ƂȂ�����ŁC���f��z=a+bi�ɑ���,z12=1, z6��1�����Ƃ���D���̂Ƃ��C �i2021�N�x�_�ސ�� ���E�H�w���j
�Ƃ����ƁC�h�E���A�u���̒藝�ɂ�� ����ɂ�� ���Ȃ킿 �܂��C �ɂ�� ���Ȃ킿 ab<0����0��θ<2π�͑�Q�C�S�ی��̊p�ŁC(2)(3)���� �i |
|
�y���7�z������
���̖₢�ɓ�����D (1)�@ (2)�@ (3)�@ �i2018�N�x���É��H�Ƒ� �H�w���j
|
|
(1) �m�����ǂށn
������āCz�̂Q�������������� z���Ɍ`���ŏ����� �܂��� �@�̂Ƃ� �A�̂Ƃ��C�قړ��l�ɂ��� �ȏ�ɂ��C�@�A�̂�����̏ꍇ���Cα=−1����i���j |
|
(2) �m�����ǂށn z≠0 (r≠0)�̂Ƃ� ���ꂪ�����ƂȂ�̂� ���Ȃ킿�Cr=1�܂���θ=nπ, r>0 ����āu���_�𒆐S�Ƃ��锼�a�P�̉~�v�܂��́u�����i�������C���_�������j�v����i���j |
|
(3) �m�����ǂށn 
�@z��(2)�̌��ʂɎ������悤�Ɂu���_�𒆐S�Ƃ��锼�a�P�̉~�v�܂��́u�����i�������C���_�������j�v�̏�̓_ �@w�́C�_ |
|
�y���8�z������
�@���f��z�� �Ƃ���D�������Ci�͋����P�ʂƂ���D�܂��C �Ƃ����D���̖�(1)�`(6)�ɓ�����D���ɂ́C���������łȂ��r���o�߂��������ƁD (1)�@ (2)�@ (3)�@A=a+b+c�͗L�����ɂȂ�D���̒l�����߂�D (4)�@B=a2+b2+c2�͗L�����ɂȂ�D���̒l�����߂�D (5)�@C=ab+bc+ca�͗L�����ɂȂ�D���̒l�����߂�D (6)�@D=a3+b3+c3−3abc�͗L�����ɂȂ�D���̒l�����߂�D �i2021�N�x������ ���w���j
|
|
�m�����ǂށn
(1) �h�E���A�u���̒藝�ɂ�� (2) ������z�C���䂪z (��1)�C������6�̓��䐔��̘a�����߂� ������(1)�̌��ʂ��g����z7=1�Ƃ���� (3) ������(2)�̌��ʂ��g���� �Ƃ���� |
|
�m�����ǂށn
(4) ������(1)�̌��ʂ��g����z7=1�Ƃ���� �����̕����̕���ƕ��q��z���|����� (5) �@A2=B+2C������ �@1=5+2C �@C=−2����i���j (6) �@D=a3+b3+c3−3abc �@=(a+b+c)(a2+b2+c2−ab−bc−ca) �@=A(B−C)=−1×(5+2)=−7����i���j |
|
�y���9�z������
�m�����ǂށn�@���������Ƃ��Cn�𐮐��Ƃ���Dz=sinθ+icosθ�Ƃ����Ƃ��C���f��zn�̎����Ƌ�����cos(nθ)��sin(nθ)��p���ĕ\���D�������Ci�͋����P�ʂł���D �i2021�N�x���s�H�|�@�ۑ� �H�|�Ȋw���j
z=cosθ+isinθ�ł���C�h�E���A�u���̒藝���̂��̂ƂȂ邪�Cz=sinθ+icosθ�Ə����Ă��邱�Ƃɒ��ӁI
�ł��邩��C�h�E���A�u���̒藝�ɂ�� �A�j n=4k(k�͐���)�̂Ƃ� �C�j n=4k+1(k�͐���)�̂Ƃ� �E�j n=4k+2(k�͐���)�̂Ƃ� �G�j n=4k+3(k�͐���)�̂Ƃ� ��p���āC���̂悤�ɂ܂Ƃ߂邱�Ƃ��ł���D
��蕶�ŁC�����Ƌ������Ď������Ƃ����߂��Ă��邩��C���ꂢ�ɂ܂Ƃ߂��Ă��C���̂܂ܓ����ɂ͂ł��Ȃ��D�����܂ł��Q�l�D
|
|
�m�����ǂށn
�i�ʉ��j
�Ƃɂ���
������ �h�E���A�u���̒藝�ɂ��
��蕶�ŁC�����Ƌ������Ď������Ƃ����߂��Ă��邩��C���ꂢ�ɂ܂Ƃ߂��Ă��C���̂܂ܓ����ɂ͂ł��Ȃ��D�����܂ł��Q�l�D
|
|
�y���10�z������
�@�ȉ��̖�ɓ�����D�������Ci�͋����P�ʂƂ���D (1)�@���f��ω= �@�@1. −20�@2. −10�@3. 10�@4. 20 �@�@5. ��̂S�̓��͂ǂ���������Ȃ��D (2)�@ �@�@1. −2�@2. −1�@3. 1�@4. 2 �@�@5. ��̂S�̓��͂ǂ���������Ȃ��D (3)�@���f�� �@�@1. −5096�@2. −4096�@3. −3096�@4. −2096 �@�@5. ��̂S�̓��͂ǂ���������Ȃ��D �i2021�N�x�h�q���j
|
|
�m�����ǂށn
(1) ω�͂P�̋����R�捪�i�̂����̂P�j�ł��邩��C���̎������藧�D
ω2+ω+1=0���(A)
ω3=1���(B)
���̖��́C�L���ʼn���I����ł��邩��C�r���o�߂̋L�q�͕s�v�ł��邪�C�����L�q���Ȃ�Cω�̐����́C���̂悤�Ɏ����悢�D
a+b=3ω2+ω+ω2+3ω=4(ω2+ω)=−4��P���v�Z�Ŏ����ꍇ�� ��� �܂� ��h�E���A�u���̒藝���g���Ď����ꍇ�� ��� ab=(3ω2+ω)(ω2+3ω)=3ω4+10ω3+3ω2 =3ω+10+3ω2=3(ω2+ω)+10=−3+10=7 a3+b3=(a+b)(a2−ab+b2)=(a+b){(a+b)2−3ab} =−4×(16−21)=20 → 4.����i���j |
|
�m�����ǂށn
(2) �h�E���A�u���̒藝�ɂ�� (3)
�O�p���̉��@�藝�̊�{���K�̂Ƃ���
�� �������o��������C���ʂ��𗧂Ă₷���ł��傤�D�������C�ׂ��Ȑ����܂ł͊o���Ă��Ȃ��Ă��悢�D ���Ɍ`���ɂ��邽�߂ɁC�܂���Βl���v�Z���Ă��� ������ �Ƃ����� �ȏォ�� ���ꂪ�����ƂȂ�ɂ́C ���̂Ƃ� |
|
�y���11�z������
�@ω�͕��f����ω5=1�����Cω=cosθ+isinθ (0��θ<2π)�ƋɌ`���\�������Ƃ��Ccosθ>0, sinθ>0�ł���Ƃ���D���̂Ƃ��Cθ=�A�ƂȂ�C1+ω+ω2+ω3+ω4=�C�ł���D �@���f��z�ɑ��� (1−ωz)(1−ω2z)(1−ω3z)(1−ω4z) =1+�Ez+�Gz2+�Iz3+�Jz4 �ł���̂ŁCα�����f���ł���Ƃ��Cz=α, ωα, ω2α, ω3α, ω4α�������邱�Ƃɂ���� (1−ωα)(1−ω2α)(1−ω3α)(1−ω4α) +(1−ωα)(1−ω2α)(1−ω3α)(1−ω5α) +(1−ωα)(1−ω2α)(1−ω4α)(1−ω5α) +(1−ωα)(1−ω3α)(1−ω4α)(1−ω5α) +(1−ω2α)(1−ω3α)(1−ω4α)(1−ω5α) =�L�@���(��) �ƂȂ�D �@���ɁC (1−ωα)(1−ω2α)(1−ω3α)(1−ω4α)(1−ω5α) =�N−i�P�@���(����) �ƂȂ�D���̂Ƃ��C��(��)�C(����)�ɒ��ӂ���� =�R+i�T �ƂȂ�D �i�A�`�T�ɂ͎���������邱�Ɓj �i2021�N�x�����ّ� ���H�E��H�w���j
|
|
�m�����ǂށn
�@�h�E���A�u���̒藝�ɂ�� ω5=cos5θ+isin5θ=1 �܂� 0��θ<2π, cosθ>0, sinθ>0 �ɂ��Cθ�͑�1�ی��̊p \( \displaystyle 5\theta=2\pi \) �@1+ω+ω2+ω3+ω4�́C������1�C���䂪ω (��1)�C������5�̓��䐔��̘a������ 1+ω+ω2+ω3+ω4= �����ŁC����ɂ��ω5=1������ 1+ω+ω2+ω3+ω4=0→�C (1−ωz)(1−ω2z)(1−ω3z)(1−ω4z) =(1−ωz)(1−ω4z)×(1−ω2z)(1−ω3z) =(1−ωz−ω4z+ω5z2)×(1−ω2z−ω3z+ω5z2) ω5=1���g�� ={1−(ω+ω4)z+z2}×{1−(ω2+ω3)z+z2} =1−(ω+ω4+ω2+ω3)z+(1+1+ω3+ω6+ω4+ω7)z2 −(ω+ω4+ω2+ω3)z3+z4 z, z3�̌W���� �C→ −(ω+ω4+ω2+ω3)=−(1+ω+ω2+ω3+ω4)+1=0+1=1 z2�̌W���� 2+ω3+ω6+ω4+ω7=2+(ω3+ω+ω4+ω2) =2+(0−1)=1 ���� (1−ωz)(1−ω2z)(1−ω3z)(1−ω4z)=1+z+z2+z3+z4→�E�G�I�J |
|
�m�����ǂށn
�E�G�I�J�̌��ʂɑ��� •z=α,��������� (����)=(1−ωα)(1−ω2α)(1−ω3α)(1−ω4α)������ӑ�1�� (�E��)=1+α+α2+α3+α4 •z=ωα,��������� (����)=(1−ω2α)(1−ω3α)(1−ω4α)(1−ω5α)�c���ӑ�5�� (�E��)==1+ωα+ω2α2+ω3α3+ω4α4 •z=ω2α,��������� (����)=(1−ω3α)(1−ω4α)(1−ω5α)(1−ω6α) =(1−ω3α)(1−ω4α)(1−ω5α)(1−ωα)������ӑ�4�� (�E��)==1+ω2α+ω4α2+ω6α3+ω8α4 =1+ω2α+ω4α2+ωα3+ω3α4 •z=ω3α,��������� (����)=(1−ω4α)(1−ω5α)(1−ω6α)(1−ω7α) =(1−ω4α)(1−ω5α)(1−ωα)(1−ω2α)������ӑ�3�� (�E��)==1+ω3α+ω6α2+ω9α3+ω12α4 =1+ω2α+ω4α2+ωα3+ω3α4 •z=ω4α,��������� (����)=(1−ω5α)(1−ω6α)(1−ω7α)(1−ω8α) =(1−ω5α)(1−ωα)(1−ω2α)(1−ω3α)������ӑ�2�� (�E��)==1+ω4α+ω8α2+ω12α3+ω16α4 =1+ω4α+ω3α2+ω2α3+ω3α4
���ӂ̘a�́C��蕶�Ɠ������D
(�E�ӂ̘a)=5+α(1+ω+ω2+ω3+ω4)���̂悤�ȓ_�����ɂ��������ɕ��ׂĂ���Ӑ}�́C�^�₾����� +α2(1+ω+ω2+ω3+ω4) +α3(1+ω+ω2+ω3+ω4) +α4(1+ω+ω2+ω3+ω4) �����ŁC�C�̌��ʂ���1+ω+ω2+ω3+ω4=0������ (�E�ӂ̘a)=5→�L |
|
�m�����ǂށn
�E�G�I�J�̌��ʂ��� (1−ωα)(1−ω2α)(1−ω3α)(1−ω4α)=1+α+α2+α3+α4 (1−ωα)(1−ω2α)(1−ω3α)(1−ω4α)(1−α)=1−α5 (1−ωα)(1−ω2α)(1−ω3α)(1−ω4α)(1−ω5α)=1−α5 �h�E���A�u���̒藝�ɂ�� (��)���̕ӁX��(����)�Ŋ���� |
|
�y���12�z������
�@����(1),(2),(3)�ɂ����ẮC�@���̂P�̃J�^�J�i��0����9�܂ł̐������P���Ă͂܂�D���̐������p�}�[�N�V�[�g�Ɂi�ȗ��j�Ƀ}�[�N���Ȃ����D�^����ꂽ�g����菭�Ȃ����̐������Ă͂܂�ꍇ�́C��ʂ̌���0�Ƃ��āC�E�ɋl�߂����l�Ƃ��Ȃ����D�����͊����Ƃ��C�l�������̏ꍇ�͕�����P�Ƃ��Ȃ����D�������܂ޕ��Ƃʼn���ꍇ�́C�����̒��Ɍ���鎩�R�����ŏ��ƂȂ�`�œ����Ȃ����D (1) ���f��α���Cα=4+4i�Ƃ����D�܂��C���f�����ʏ��|z−α|=
(a)β=�A−���C+i(�E+���G)
γ=�I+���J+i(�L−���N) �ł���D �܂�,β�̕Ίp��
(b)�@1��n��2021�������R��n�̂����Cγn���������ƂȂ�悤��n�̌��́C�\�^�`�ł���D (c)|z−α|= �i2021�N�x�������ȑ� �H�w���j
2021�Ƃ��������ɐ��w�I�ɓ��ʂȈӖ�������킯�ł͂Ȃ��C�K���ɑ傫�Ȑ����̒�����C���w�����̔N�x���g���āC�W���[�N�Ƃ��Ďg���Ă�����̂ƍl������D
----- �M���V�������̓ǂݕ��F |
|
(a) �m�����ǂށn  �@α=4+4i�𒆐S�Ƃ��锼�a
�@α=4+4i�𒆐S�Ƃ��锼�a�@���̒��p�O�p�`ABO�ɂ����āC�O�����̒藝��p����OB�̒��������߂�ƁC �@���������āCβ�̕Ίp�� �@γ�̕Ίp�� �@ �����ŁC�O�p���̉��@�藝�ɂ�� |
|
�m�����ǂށn |
|
(b) �m�����ǂށn
γ�̕Ίp�� ���ꂪ�������ɂȂ�̂� �̂Ƃ��D���Ȃ킿 n=12k+6(k�͐���, 1��n��2021) 1��12k+6��2021(k�͐���) k�͐��������� �@�@168��→�\�^�`
���������l����C�����邪�C�u����R��100���̂����ŁC�{���15������20���ʼn����v���Ƃ͂ƂĂ����
|
|
(c) �m�����ǂށn
z�̕Ίp��θ�Ƃ����� zn���������ƂȂ�̂́C 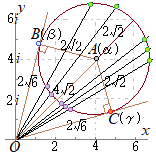 �@�E�}�̂悤��
�@�E�}�̂悤���@�@2×674=1348��→�c�e�g�i |
|
�y���13�z������
�@i�������P�ʂƂ��C a, b�𐳂̐����Ƃ��C���f�� �i2021�N�x�k���� ��w���j
|
|
�m�����ǂށn
���ꂼ��̕��f�����Ɍ`���ɒ����� 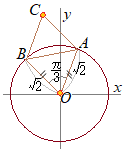 ������
�������ƂȂ��āC����AB���P�ӂƂ��鐳�O�p�`ABC�́C�P�̒��_�͌��_O�ɂȂ�D�����P�̒��_C��\�����f���� ���̎����� ��Q�����O�p���̉��@�藝��p���Čv�Z����ƁC ���߂������ |
|
�m�����ǂށn �̂P�̕Ίp�́in�͐����Ƃ��āj �A�j 14−3a+4b=1 (a, b��1)�̂Ƃ� 3a−4b=13���(1) �P�̉��� 3×7−4×2=13���(2) (1)−(2) 3(a−4)=4(b−2) ���̂Ƃ� 3, 4�݂͌��ɑf������ a−7=4t a=4t+7 (t��−1) b−2=3t b=3t+2 (t��0) a+b=7t+9 (t��0) ���̏ꍇ�̍ŏ��l��9 �C�j 14−3a+4b=25 (a, b��1)�̂Ƃ� 4b−3a=11���(3) �P�̉��� 4×5−3×3=11���(4) (3)−(4) 4(b−5)=3(a−3) ���̂Ƃ� 3, 4�݂͌��ɑf������ a−3=4t a=4t+3 (t��0) b−5=3t b=3t+5 (t��−1) a+b=7t+8 (t��0) ���̏ꍇ�̍ŏ��l��8  �@a��1, b��1�ƂȂ�̂́C�E�}�̐��F�͈̔́i���E�����܂ށj
�@a��1, b��1�ƂȂ�̂́C�E�}�̐��F�͈̔́i���E�����܂ށj���̂����ŁC �@�A�j14−3a+4b=1 (a, b��1)�̂Ƃ��Ca+b�̍ŏ��l��9 �@�C�j14−3a+4b=25 (a, b��1)�̂Ƃ��Ca+b�̍ŏ��l��8 �@�E�j14−3a+4b��−23 (a, b��1)��14−3a+4b��49 (a, b��1)�̂Ƃ��Ca+b�̍ŏ��l�̓A�j�C�j�̏ꍇ�����傫���Ȃ�D �@�ȏ�ɂ��C�C�j�̏ꍇ����C�ŏ��l��8→�N����i���j |
|
���L�̃����N���g���ă��j���[�ɖ߂��Ă��������D |