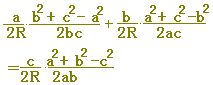三角形の形状・証明問題

このページのマイナーチェンジありカバー版ページ
（グーグルブロガー版）は，こちら⇒

==正弦定理・余弦定理の応用 - 三角形の形状・証明問題 == 《解説》
□
　三角形の形状問題（正三角形，二等辺三角形，直角三角形など三角形の種類を言い当てる問題）や証明問題においては，正弦定理や余弦定理を変形して，角度に関する式を辺に関する式に直してから考えるのが原則です．
＜原則＞・・・角を辺に直す

・
・
・tanＡは上記２つを用いてとします．

Ｂ，Ｃについても同様です．

　角度の関係式を辺の関係式に直すのは，一般に角度の関係式が変形しにくく，見通しを立てにくいからです：

例　sin(A+B)やsinAcosB-sinBcosAは変形しにくいが
　(a+b)²=a²+2ab+b²においては，文字式の通常の展開公式が使えます．

　例
　次の等式が成り立つとき，この△ＡＢＣはどんな形の三角形か．
　asinA=bsinB+csinC

　(答案)

　などを代入すると，

これより，ａ^２＝ｂ^２＋ｃ^２　
∠Ａ＝９０゜の直角三角形・・・(答)

□　最後の詰めは，どうするのか
　辺だけの関係式から，三角形の形状を言い当てるには，次のような性質を用います．
a=b　→　∠Ａ＝∠Ｂの二等辺三角形

（b=c，ｃ＝ａについても同様）

ａ＝ｂ＝ｃ　→　正三角形

辺についての関係式から「直角」など角度についての関係を引き出すには，「ピタゴラスの定理の逆」を前もって覚えておかなければできません．
ａ^２＝ｂ^２＋ｃ^２　→　∠Ａ＝９０゜の直角三角形

（b=c，ｃ＝ａについても同様）

ａ^２＝ｂ^２＋ｃ^２　かつ　ｂ＝ｃ　→　∠Ａ＝９０゜の直角二等辺三角形
　答案としては，単に「二等辺三角形」とするのではなく「∠Ａ＝∠Ｂの二等辺三角形」，単に「直角三角形」とするのではなく「∠Ａ＝９０゜の直角三角形」と書くことが要求されるのが普通です．　

《問題》　次の等式が成り立つとき，この△ＡＢＣはどんな形の三角形か　 1 sin²A=sin²B+sin²C などを代入すると，となり，分母を払うとａ^２＝ｂ^２＋ｃ^２となります．	ａ＝ｂの二等辺三角形ｂ＝ｃの二等辺三角形ｃ＝ａの二等辺三角形正三角形 ∠Ａ＝90゜の直角三角形 ∠Ｂ＝90゜の直角三角形 ∠Ｃ＝90゜の直角三角形 ∠Ａ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
２　*ｃ＝２ａcosＢ* を代入となりｃ^２＝ｃ^２＋ａ^２－ｂ^２ａ^２＝ｂ^２ａ，ｂ＞０だからａ＝ｂ	ａ＝ｂの二等辺三角形ｂ＝ｃの二等辺三角形ｃ＝ａの二等辺三角形正三角形 ∠Ａ＝90゜の直角三角形 ∠Ｂ＝90゜の直角三角形 ∠Ｃ＝90゜の直角三角形 ∠Ａ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
３　*ａsinＡ＝(b+c)(sinB-sinC)* などを代入すると，となり，分母を払うとａ^２＝ｂ^２－ｃ^２となります．ここで-c²を移項します．	ａ＝ｂの二等辺三角形ｂ＝ｃの二等辺三角形ｃ＝ａの二等辺三角形正三角形 ∠Ａ＝90゜の直角三角形 ∠Ｂ＝90゜の直角三角形 ∠Ｃ＝90゜の直角三角形 ∠Ａ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
４　sinAcosB=sinBcosA ，などを代入すると移項すると，２（ａ^２－ｂ^２）＝０ａ，ｂ＞０だからａ＝ｂ	ａ＝ｂの二等辺三角形ｂ＝ｃの二等辺三角形ｃ＝ａの二等辺三角形正三角形 ∠Ａ＝90゜の直角三角形 ∠Ｂ＝90゜の直角三角形 ∠Ｃ＝90゜の直角三角形 ∠Ａ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
５　*２cosBsinC=sinA* ，などを代入するとこれよりｃ^２＋ａ^２－ｂ^２＝ａ^２つまりｃ^２－ｂ^２＝０ｃ，ｂ＞０だからｃ＝ｂ	ａ＝ｂの二等辺三角形ｂ＝ｃの二等辺三角形ｃ＝ａの二等辺三角形正三角形 ∠Ａ＝90゜の直角三角形 ∠Ｂ＝90゜の直角三角形 ∠Ｃ＝90゜の直角三角形 ∠Ａ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)

《解説》
□　変形していくと，３次式，４次式，．．．となることがあります．このような場合，因数分解によって判断します．
　例
　　(ａ^２－ｂ^２)(ａ^２＋ｂ^２－ｃ^２)＝０となれば「ａ＝ｂの二等辺三角形」又は「∠Ｃ＝90゜の直角三角形」とします．
□　ｃｏｓ^２Ａなどに上記の変形をそのまま代入すると，となって複雑になりすぎます．この場合，ｃｏｓ^２Ａ＝１－sin^２Aとして，を用いることができます．

《問題つづき》６ sinAcosA+sinBcosB=sinCcosC ，などを代入すると分母を払って移項するとａ^４－２ａ^２ｂ^２＋ｂ^４－ｃ^４＝０ (ａ^２－ｂ^２)^２－ｃ^４＝０ (ａ^２－ｂ^２＋ｃ^２)(ａ^２－ｂ^２－ｃ^２)＝０	ａ＝ｂ又はｂ＝ｃの二等辺三角形ｂ＝ｃ又はｃ＝ａの二等辺三角形ｃ＝ａ又はａ＝ｂの二等辺三角形正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
◇７ $(b-c)\cos^2A=b\cos^2B-c\cos^2C$ $cos^2A=1-\sin^2A$ などを代入すると $(b-c)(1-\sin^2A)=b(1-\sin^2B)-c(1-\sin^2C)$ ここで $1-\sin^2A=1-(\frac{a}{2R})^2$ などを代入して簡単にする $(b-c)\{1-(\frac{a}{2R})^2\}$ $=b\{1-(\frac{b}{2R})^2\}-c\{1-(\frac{c}{2R})^2\}$ $(b-c)-(b-c)(\frac{a}{2R})^2$ $=b-b(\frac{b}{2R})^2)-c-c(\frac{c}{2R})^2)$ $-(b-c)(\frac{a}{2R})^2=-b(\frac{b}{2R})^2)-c(\frac{c}{2R})^2)$ $(b-c)a^2=b^3-c^3$ $(b-c)(a^2-b^2-bc-c^2)=0$ ゆえに $b=c$ または $a^2-b^2-bc-c^2=0$ ここで， $a^2=b^2+ bc+ c^2$ は $a^2-b^2-bc-c^2=0$ を表すすなわち， $\cos A=-\frac{1}{2}$ を表す結局, $b=c$ の二等辺三角形または $A=120^{\circ}$ の(鈍角)三角形	ａ＝ｂ又はｂ＝ｃの二等辺三角形ｂ＝ｃ又はｃ＝ａの二等辺三角形ｃ＝ａ又はａ＝ｂの二等辺三角形正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
◇８　tanＡ：tanB=ａ^２：ｂ^２ｂ^２tanＡ＝ａ^２tanＢｂ^２sinＡ/cosA＝ａ^２sinＢ/cosB b²(c²+a²-b²)=a²(b²+c²-a²) b²c²+b²a²-b⁴-a²b²-a²c²+a⁴=0 b²c²-b⁴-a²c²+a⁴=0 (b²-a²)(c²-a²-b²)=0	ａ＝ｂ又はｂ＝ｃの二等辺三角形ｂ＝ｃ又はｃ＝ａの二等辺三角形ｃ＝ａ又はａ＝ｂの二等辺三角形正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)

←メニューに戻る

《問題つづき》６ sinAcosA+sinBcosB=sinCcosC ，などを代入すると分母を払って移項するとａ^４－２ａ^２ｂ^２＋ｂ^４－ｃ^４＝０ (ａ^２－ｂ^２)^２－ｃ^４＝０ (ａ^２－ｂ^２＋ｃ^２)(ａ^２－ｂ^２－ｃ^２)＝０	ａ＝ｂ又はｂ＝ｃの二等辺三角形ｂ＝ｃ又はｃ＝ａの二等辺三角形ｃ＝ａ又はａ＝ｂの二等辺三角形正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
◇７ $(b-c)\cos^2A=b\cos^2B-c\cos^2C$ $cos^2A=1-\sin^2A$ などを代入すると $(b-c)(1-\sin^2A)=b(1-\sin^2B)-c(1-\sin^2C)$ ここで $1-\sin^2A=1-(\frac{a}{2R})^2$ などを代入して簡単にする $(b-c)\{1-(\frac{a}{2R})^2\}$ $=b\{1-(\frac{b}{2R})^2\}-c\{1-(\frac{c}{2R})^2\}$ $(b-c)-(b-c)(\frac{a}{2R})^2$ $=b-b(\frac{b}{2R})^2)-c-c(\frac{c}{2R})^2)$ $-(b-c)(\frac{a}{2R})^2=-b(\frac{b}{2R})^2)-c(\frac{c}{2R})^2)$ $(b-c)a^2=b^3-c^3$ $(b-c)(a^2-b^2-bc-c^2)=0$ ゆえに $b=c$ または $a^2-b^2-bc-c^2=0$ ここで， $a^2=b^2+ bc+ c^2$ は $a^2-b^2-bc-c^2=0$ を表すすなわち， $\cos A=-\frac{1}{2}$ を表す結局, $b=c$ の二等辺三角形または $A=120^{\circ}$ の(鈍角)三角形	ａ＝ｂ又はｂ＝ｃの二等辺三角形ｂ＝ｃ又はｃ＝ａの二等辺三角形ｃ＝ａ又はａ＝ｂの二等辺三角形正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)
◇８　tanＡ：tanB=ａ^２：ｂ^２ｂ^２tanＡ＝ａ^２tanＢｂ^２sinＡ/cosA＝ａ^２sinＢ/cosB b²(c²+a²-b²)=a²(b²+c²-a²) b²c²+b²a²-b⁴-a²b²-a²c²+a⁴=0 b²c²-b⁴-a²c²+a⁴=0 (b²-a²)(c²-a²-b²)=0	ａ＝ｂ又はｂ＝ｃの二等辺三角形ｂ＝ｃ又はｃ＝ａの二等辺三角形ｃ＝ａ又はａ＝ｂの二等辺三角形正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形上記のいずれでもない (ヒントがほしい)