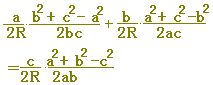|
《解説》 ○三角形の形状問題（正三角形，二等辺三角形，直角三角形など三角形の種類を言い当てる問題）や証明問題においては，正弦定理や余弦定理を変形して，角度に関する式を辺に関する式に直してから考えるのが原則です． ＜原則＞・・・角を辺に直す
⇒
Ｂ，Ｃについても同様です．
⇒ 
⇒tanＡは上記２つを用いて とします． （「辺→角」でなく「角→辺」に変形する理由） 角度の関係式を辺の関係式に直すと，一般に角度の関係式が変形しにくく，見通しを立てにくいからです：
【例】
のような角度を含む式は変形しにくいが のような辺だけを含む式は，文字式の通常の展開公式が使える． |
|
例
次の等式が成り立つとき，この△ＡＢＣはどんな形の三角形か．
(答案)
などを代入すると， これより，ａ２＝ｂ２＋ｃ２ ∠Ａ＝９０゜の直角三角形・・・(答) |
|
□ 最後の詰めは，どうするのか
辺だけの関係式から，三角形の形状を言い当てるには，次のような性質を用います．
○a=b → ∠Ａ＝∠Ｂの二等辺三角形
（b=c，ｃ＝ａについても同様）
○ａ＝ｂ＝ｃ → 正三角形
辺についての関係式から「直角」など角度についての関係を引き出すには，「ピタゴラスの定理の逆」を前もって覚えておかなければできません．
○ａ２＝ｂ２＋ｃ２ → ∠Ａ＝９０゜の直角三角形
（b=c，ｃ＝ａについても同様）
○ａ２＝ｂ２＋ｃ２ かつ ｂ＝ｃ→ ∠Ａ＝９０゜の直角二等辺三角形 答案としては，
単に「二等辺三角形」とするのではなく「∠Ａ＝∠Ｂの二等辺三角形」，
などと書くことが要求されます．
単に「直角三角形」とするのではなく「∠Ａ＝９０゜の直角三角形」 |
|
《解説》
○変形していくと，３次式，４次式，．．．となることがあります．このような場合，因数分解によって判断します． 【例】
(ａ２−ｂ２)(ａ２＋ｂ２−ｃ２)＝０
となれば
ａ＝ｂの二等辺三角形
とします．または ∠Ｃ＝90゜の直角三角形 ○角を辺に直す場合に注意すべきこととして， となって複雑になりすぎます．このような場合， として， に直すことができます． |
|
《問題つづき》 ６ 
【選択肢】
ａ＝ｂ又はｂ＝ｃの二等辺三角形
ｂ＝ｃ又はｃ＝ａの二等辺三角形 ｃ＝ａ又はａ＝ｂの二等辺三角形 正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形 上記のいずれでもない (ヒントがほしい) ，
などを代入すると 
分母を払って移項すると ａ４−２ａ２ｂ２＋ｂ４−ｃ４＝０ (ａ２−ｂ２)２−ｃ４＝０ (ａ２−ｂ２＋ｃ２)(ａ２−ｂ２−ｃ２)＝０ |
| ◇７
【選択肢】
ａ＝ｂ又はｂ＝ｃの二等辺三角形
ｂ＝ｃ又はｃ＝ａの二等辺三角形 ｃ＝ａ又はａ＝ｂの二等辺三角形 正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形 上記のいずれでもない (ヒントがほしい) ここで ゆえに
ここで，
結局,すなわち， |
| ◇８
【選択肢】
ａ＝ｂ又はｂ＝ｃの二等辺三角形
ｂ＝ｃ又はｃ＝ａの二等辺三角形 ｃ＝ａ又はａ＝ｂの二等辺三角形 正三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角三角形 ∠Ａ＝90゜又は∠Ｂ＝90゜の直角二等辺三角形 ∠Ｂ＝90゜又は∠Ｃ＝90゜の直角二等辺三角形 ∠Ｃ＝90゜又は∠Ａ＝90゜の直角二等辺三角形 上記のいずれでもない (ヒントがほしい) ｂ２tanＡ＝ａ２ｔａｎＢ
ｂ２sinＡ/cosA＝ａ２sinＢ/cosB  b2(c2+a2-b2)=a2(b2+c2-a2) b2c2+b2a2-b4-a2b2-a2c2+a4=0 b2c2-b4-a2c2+a4=0 (b2-a2)(c2-a2-b2)=0 |
 (携帯版)...メニューに戻る...（PC版）メニューに戻る |
となり，
となり
となり，
