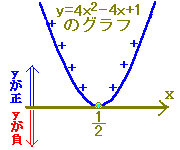
|
・・・2次関数のグラフがx軸と1点で接する場合 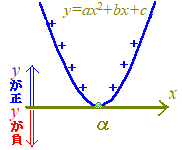 <問題の形> <答の形> ア) ax2+bx+c<0 (a>0) → 解なし
0以上のものしかないときに、負のものを探してもない
イ) ax2+bx+c>0 (a>0) → x<α, α<x
ax2+bx+c≦0とは,「負でもよい」「0でもよい」ということ
エ) ax2+bx+c≧0 (a>0) → xはすべての数
グラフを見ると, 「負のところ」→ない,「0のところ」→1つだけある: x=αだけが解)
0以上のものばかりのときに、0以上のものを探せば
(参考) ax2+bx+cは2次式
2次式には「解」などというものはない.2次式は,展開や因数分解などの式の変形ができるだけである.
ax2+bx+c=0は2次方程式
2次方程式の解は,因数分解や解の公式を使って求めることができる.2次方程式の解はxの「値」になる.
ax2+bx+c≧0,ax2+bx+c<0などは2次不等式※見た目で言えば,2次式に=0を付けたら2次方程式になる.
2次不等式の解は,一般にはxの「値の範囲」になる.
y=ax2+bx+cは2次関数※見た目で言えば,2次式に <0, ≦0, >0, ≧0を付けたら2次不等式になる.
2次関数には「グラフ」が対応する.
※見た目で言えば,2次式にy=を付けたら2次関数になる. 右上に続く↑
|
■2次不等式の解き方の流れ (1) 初めに「2次不等式」の問題が与えられたとき
【例】x2−4x+3<0
(2) 2次不等式を解くためには「2次関数」のグラフを描かなければならない.
【例】y=x2−4x+3
(3) 2次関数のグラフとx軸との交点を求めるには,2次方程式」を解かなければならない.
【例】x2−4x+3=0
 実際に問題を解くときは,上記の考察を「逆順」にたどればよい.
実際に問題を解くときは,上記の考察を「逆順」にたどればよい.初めに問題を見たら (3)2次方程式を作る x2−4x+3=0  2次方程式の解を求める x=1, 3  (2) 2次関数 y=x2−4x+3 のグラフを描く(右図)  (1) 2次不等式の解を求める 1<x<3…(答) ※2次不等式を見せられたら,誰も聞いていないのに
「2次方程式は〜♪」
と一人演説をしなければならない.「2次方程式の解は〜♪」 「2次関数のグラフは〜♪」 この一人演説の長さに耐えられなければ,問題は解けない. ※次の違いにも注意してください ⇒ 2次方程式の解は2次不等式の解とは違う. (ここでは2次不等式が目的で,2次方程式は手段) |
|
【例題1】
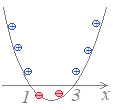
(解答)2次不等式x2−4x+3<0の解を求めてください.  2次方程式
2次方程式x2−4x+3=0 の解は x=1, 3 2次関数 y=x2−4x+3 のグラフは右図のようになる. グラフからy<0になるxの値の範囲は 1<x<3…(答)
※要約のところで,ア)イ)ウ)エ)に付いていたa>0は何の役にたっているのか.
たとえば,a<0の場合とは−x2+4x−3>0のようにx2の係数が負の数になっているとき,そのまま y=−x2+4x−3 のグラフを使って解くと,グラフの凹凸が逆になって混乱する場合があるので,基本を固める段階では −x2+4x−3>0 のような形の問題は,両辺に−1を掛けるとか,左辺の式を右辺に移項するなどして x2−4x+3<0 に直してから解くということです. |
【例題2】
(解答)2次不等式x2−8x+16>0の解を求めてください. 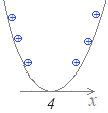 2次方程式
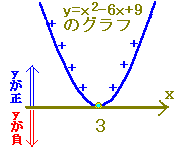
2次方程式x2−8x+16=0 (x−4)2=0 の解は x=4(重解) だから,2次関数 y=x2−8x+16 のグラフは右図のようになる. グラフからy>0になるxの値の範囲は x<4, 4<x…(答) (注:x≠4と書いてもよい) |
|
|
||||||||
|
|
||||||||
|
|
||||||||