→ 携帯用は別頁

【平均変化率】
(1)　
xの値がaからbまで変化するときの関数y=f(x)の値の平均変化率は
${\displaystyle \frac{f(b)-f(a)}{b-a}}$
(2)　
xの値がaからa+hまで変化するときの関数y=f(x)の値の平均変化率は
${\displaystyle \frac{f(a+h)-f(a)}{h}}$

【例題1】
　関数f(x)=3x2+2x−4について，xの値が1から3まで変化するときの平均変化率を求めてください．

【問題1-1】
　関数f(x)=2x2+3x+4について，xの値が0から3まで変化するときの平均変化率を求めてください．

（解答）
${\displaystyle \frac{f(3)-f(0)}{3-0}}={\displaystyle \frac{31-4}{3}}=9$･･･（答）
→解説を隠す←

【問題1-2】
　関数f(x)=−2x+3の区間(−1≦x≦2)における平均変化率を求めてください．

（解答）
${\displaystyle \frac{f(2)-f(-1)}{2-(-1)}}={\displaystyle \frac{-1-5}{3}}=-2$･･･（答）
→解説を隠す←

【問題1-3】
　関数f(x)=x2−2x+3xの値がaからbまで変化するときの平均変化率を求めてください．（ただし，a<bとする）
a+b−

（解答）
${\displaystyle \frac{f(b)-f(a)}{b-a}}={\displaystyle \frac{(b^2-2b+3)-(a^2-2a+3)}{b-a}}$
$={\displaystyle \frac{(b^2-a^2)-2(b-a)}{b-a}}={\displaystyle \frac{b+a-2}{b-a}}=a+b-2$ ･･･(答)
→解説を隠す←

【数学Ⅱの答案で黙って使ってよい極限値2】
• そのまま代入すると分母が0になるときは，
「約分によって分母が0になる原因を取り除いてから」値を代入するとよい

【例題2-2】
(1)　${\displaystyle \underset{x\to 0}{lim}{\displaystyle \frac{x^2+2x}{x}}}$
(2)　${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{x^2-1}{x-1}}}$
(3)　${\displaystyle \underset{x\to 2}{lim}{\displaystyle \frac{x^2-3x+2}{x-2}}}$

x→0のときに，xで約分するということは，0で割ることにならないか？
--------
　最初の定義をよく見ると，「xの値がaと異なる値をとりながら限りなくaに近づくとき」と書いてあるので，x→0のときは，xは0以外の値をとりながら，0に近づくので，xで約分しても，0で割ったことにならないのです．

【問題2-1】
　次の極限値を求めてください．
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{x^2+x-2}{x-1}}}$=

（解答）
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{x^2+x-2}{x-1}}=\underset{x\to 1}{lim}{\displaystyle \frac{\cancel{(x-1)}(x+2)}{\cancel{x-1}}}}$
${\displaystyle =\underset{x\to 1}{lim}(x+2)=3}$･･･（答） →解説を隠す←

【問題2-2】
　次の極限値を求めてください．
${\displaystyle \underset{x\to 2}{lim}{\displaystyle \frac{x^2-4}{x^2-5x+6}}}$=

（解答）
${\displaystyle \underset{x\to 2}{lim}{\displaystyle \frac{x^2-4}{x^2-5x+6}}=\underset{x\to 2}{lim}{\displaystyle \frac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x-3)}}}$
${\displaystyle =\underset{x\to 2}{lim}{\displaystyle \frac{x+2}{x-3}}=-4}$･･･（答） →解説を隠す←

【問題2-3】
　次の極限値を求めてください．
${\displaystyle \underset{x\to 2}{lim}{\displaystyle \frac{x^3-8}{x^2-4}}}$=

（解答）
${\displaystyle \underset{x\to 2}{lim}{\displaystyle \frac{x^3-8}{x^2-4}}=\underset{x\to 2}{lim}{\displaystyle \frac{\cancel{(x-2)}(x^2+2x+4)}{\cancel{(x-2)}(x+2)}}}$
${\displaystyle =\underset{x\to 2}{lim}{\displaystyle \frac{x^2+2x+4}{x+2}}=3}$･･･（答） →解説を隠す←

【数学Ⅱの答案で黙って使ってよい極限値3】
　高校数学のやり方としては，少しずつ近づけて，どこへ向かうかが言えればよい．（直感的な考え方）

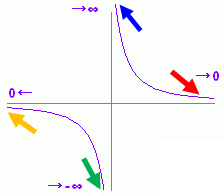
右図の赤矢印
x=10, 100, 1000, 10000, ･･･のとき
${\displaystyle \frac{1}{x}}$=0.1, 0.01, 0.001, 0.0001, ･･･となるから
${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{1}{x}}=0}$

右図の黄色矢印
x=−10, −100, −1000, −10000, ･･･のとき
${\displaystyle \frac{1}{x}}$=−0.1, −0.01, −0.001, −0.0001, ･･･となるから
${\displaystyle \underset{x\to -\mathrm{\infty }}{lim}{\displaystyle \frac{1}{x}}=0}$

（x→+0とは，0よりも大きな値をとりながら0に限りなく近づくことを言う．）
右図の青矢印
x=0.1, 0.01, 0.001, 0.0001, ･･･のとき
${\displaystyle \frac{1}{x}}$=10, 100, 1000, 10000, ･･･となるから
${\displaystyle \underset{x\to +0}{lim}{\displaystyle \frac{1}{x}}=\mathrm{\infty }}$
${\displaystyle \underset{x\to +0}{lim}{\displaystyle \frac{1}{x}}=+\mathrm{\infty }}$と書いてもよい

（x→−0とは，0よりも小さな値（負の値）をとりながら0に限りなく近づくことを言う．）
右図の緑色矢印
x=−0.1, −0.01, −0.001, −0.0001, ･･･のとき
${\displaystyle \frac{1}{x}}$=−10, −100, −1000, −10000, ･･･となるから
${\displaystyle \underset{x\to -0}{lim}{\displaystyle \frac{1}{x}}=-\mathrm{\infty }}$
（参考）
${\displaystyle \underset{x\to 0}{lim}{\displaystyle \frac{1}{x}}}$
の場合は，ア）正の値をとりながら0に近づく場合，イ）負の値をとりながら0に近づく場合，ウ）正負の値を振動しながら0に近づく場合の，いずれかによって、極限値が変わり，どの場合なのかが指定されていないから，極限値は決まらない．極限値なしとする．
　もともと，∞に近づく場合も，∞は特定の値でないので「極限なし」と書くこともあるが，「極限なし」の中でも「限りなく大きくなって，極限がない場合→+∞」「限りなく小さくなって，極限がない場合→−∞」「絶対値が限りなく大きくなるが，振動して符号が定まらない場合→±∞」のように分けることができ，無限という記号を使って表すことも多い．

【問題3-1】
　次の極限値を求めてください． ${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{1}{2x-1}}}$=

（解答）
x→∞のときt=2x−1→∞だから ${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{1}{2x-1}}=\underset{t\to \mathrm{\infty }}{lim}{\displaystyle \frac{1}{t}}=0}$･･･（答） →解説を隠す←

【問題3-2】
　次の極限値を求めてください．
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{1}{x-1}}}$=

（解答）
x=1.1, 1.01, 1.001, 1.0001, ･･･のとき
${\displaystyle \frac{1}{x}}$=10, 100, 1000, 10000, ･･･
x=0.9, 0.99, 0.999, 0.9999, ･･･のとき
${\displaystyle \frac{1}{x}}$=−10, −100, −1000, −10000, ･･･
１よりも大きな値をとりながら１に近づく場合と，１よりも小さな値をとりながら１に近づく場合とで，極限値が一致しないから，極限値は なし･･･（答） →解説を隠す←

【問題3-3】
　次の極限値を求めてください．
${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{\displaystyle \frac{2}{3x+1}}}$=

（解答）
x=10, 100, 1000, 10000, ･･･のとき
${\displaystyle \frac{2}{3x+1}}={\displaystyle \frac{2}{31}},{\displaystyle \frac{2}{301}},{\displaystyle \frac{2}{3001}},{\displaystyle \frac{2}{30001}},\cdots$
は，限りなく0に近づく
0･･･（答） →解説を隠す←

【極限値が存在するための条件】
　例えば，${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{x^2+ax+b}{x-1}}=3}$となるように定数a, bの値を定める問題では，
(1) 分母の極限値が0になるとき，分子の極限値が0以外の場合は，式の極限値が有限の値に定まらないから，「分子の極限が0になる」ということが第１の条件になる．
　　1+a+b=0
(2) 上記の条件を満たすときは，（因数定理により分子がx−1という因数をもつこといなるから），分母と分子はx−1で約分できる．そこで，「式の極限値が3になる」ということが第２の条件になる．
　　2+a=3
これら２つの条件から，連立方程式を解くと，定数a, bの値が定まる．
　　a=1, b=−2
【要点】
(1) 極限値が定まること，(2) その極限値が与えられた値になること，の２つの条件から連立方程式が解ける．

上記(1)の補足説明
　分母→1のときに
ア）分子が0以外の有限の値に近づく場合
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{1}{x-1}},\underset{x\to 1}{lim}{\displaystyle \frac{2}{x-1}},\underset{x\to 1}{lim}{\displaystyle \frac{3}{x-1}},\cdots }$
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{-1}{x-1}},\underset{x\to 1}{lim}{\displaystyle \frac{-2}{x-1}},\underset{x\to 1}{lim}{\displaystyle \frac{-3}{x-1}},\cdots }$
などは，いずれも式の値が限りなく大きく（符号は正負ともあり）なるので，有限の極限値をもたない．
イ）分子が無限大になる場合も，与えられた式が有限の極限値をもつことはない．
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{{\displaystyle \frac{1}{x-1}}}{x-1}}=\mathrm{\infty }}$など
• 以上のように，分母が0に近づくときに，分子が0以外の値に近づくと，式全体は有限な極限値をもたないので，式全体が有限な極限値をもつためには，「分子→0が必要条件」になる．
• この条件を入れると，分数の約分ができるようになるが，極限値が実際に与えられた値になるかどうかの「十分条件」も調べなければならないということです．

【例題4】
　${\displaystyle \underset{x\to 2}{lim}{\displaystyle \frac{x^2+ax+b}{x-2}}=-1}$
となるように定数a, bの値を定めてください．

【問題4-1】
　次の等式が成り立つように定数a, bの値を定めてください．
${\displaystyle \underset{x\to -1}{lim}{\displaystyle \frac{a{x}^2+bx+1}{x+1}}=3}$
a=, b=

（解答）
x→−1のとき，分母→0となるから，与えらえた式の極限値が有限の値になるためには，分子→0が必要条件となる
　a−b+1=0
そこで，b=a+1を代入して，極限値を求めると
${\displaystyle \underset{x\to -1}{lim}{\displaystyle \frac{a{x}^2+(a+1)x+1}{x+1}}=\underset{x\to -1}{lim}{\displaystyle \frac{a(x^2+x)+x+1}{x+1}}}$
${\displaystyle =\underset{x\to -1}{lim}{\displaystyle \frac{\cancel{(x+1)}(ax+1)}{\cancel{x+1}}}=-a+1=3}$
ゆえに，a=−2, b=−1･･･（答） →解説を隠す←

【問題4-2】
　次の等式が成り立つように定数a, bの値を定めてください．
${\displaystyle \underset{x\to 3}{lim}{\displaystyle \frac{x^2+3x-18}{x^2+ax+b}}={\displaystyle \frac{1}{2}}}$
a=, b=

（解答）
x→3のとき，分子→0となるから，与えらえた式の極限値が0以外の値になるためには，分母→0が必要条件となる
　9+3a+b=0
そこで，b=−3a−9を代入して，極限値を求めると
${\displaystyle \underset{x\to 3}{lim}{\displaystyle \frac{x^2+3x-18}{x^2+ax-3a-9}}=\underset{x\to -1}{lim}{\displaystyle \frac{(x-3)(x+6)}{(x-3)(x+3)+a(x-3)}}}$
${\displaystyle =\underset{x\to 3}{lim}{\displaystyle \frac{\cancel{(x-3)}(x+6)}{\cancel{(x-3)}(x+3+a)}}=\underset{x\to 3}{lim}{\displaystyle \frac{x+6}{x+3+a}}}$
$={\displaystyle \frac{9}{6+a}}={\displaystyle \frac{1}{2}}$
ゆえに，a=12, b=−45･･･（答） →解説を隠す←

【問題4-3】
　次の等式が成り立つように定数a, bの値を定めてください．
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{x^2+ax-2}{x^2-(b+1)x+b}}=1}$
a=, b=

（解答）
x→1のとき，分母→0となるから，与えらえた式の極限値が有限の値になるためには，分子→0が必要条件となる
　1+a−2=0
そこで，a=1を代入して，極限値を求めると
${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{(x+2)\cancel{(x-1)}}{\cancel{(x-1)}(x-b)}}={\displaystyle \frac{3}{1-b}}=1}$
b=−2
ゆえに，a=1, b=−2･･･（答） →解説を隠す←