|
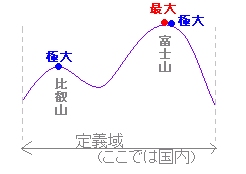
���@�ɑ�l�C�ɏ��l(�ɒl) ������� �y���Ƃ��b�ŃX�^�[�g�z ���ɑ�C�ɏ��ƍő�C�ŏ��̈Ⴂ �@��`��̒��ň�ԍ����̂��ő� �@�@�@����@���Ƃ��Εx�m�R �@�ߏ��ň�ԍ����̂��ɑ� �@�@�@����@���Ƃ��Δ�b�R�@(�x�m�R�͋ɑ傩�ő�) ���R�̒��オ�ɑ�(���̒l���ɑ�l) ���ő�l�͂����Ă��P�����ɑ�l�͕������蓾��D (�ɏ��ɂ��Ă����l�D)
�y�ɒl�z
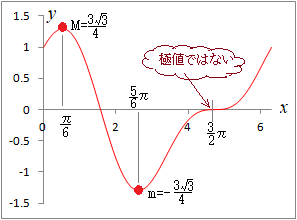
f(x) ���A�����̂Ƃ��C�������猸���ɕς��Ƃ������ɑ��Ƃ����D�������瑝���ɕς��Ƃ������ɏ��Ƃ����D �܂��C���̂Ƃ���f(x)�̒l���e�X�ɑ�l�C�ɏ��l�Ƃ����D �y�ɒl�̒��ו��z (1) f’(x) = 0�ƂȂ�Ƃ����Ɛ�Βl�L���Ȃǂ��������܂�Ă���Ƃ��������ɏグ��D (2) �e�X�̌��ɂ��āC�����C�������u�ω��v���Ă���ɒl�Ɣ��f����D ���@���_��� 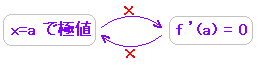 |
|
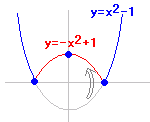
| �� f’(x) = 0 �ƂȂ�_�͋ɒl�̗L�͂Ȍ��ł����Cf’(x) = 0 ������Ƃ����ċɒl���Ƃ͌���܂���D ���̐}��y = x2 �� x = 0 �ɂ����Č������瑝���ɕω�����̂ŁC�ɏ��ł����Cy = x3 �� x = 0�ɂ����đ������瑝���ɂȂ�̂ŁC�ɒl�ł͂���܂���D 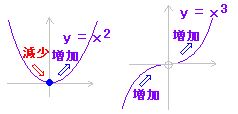 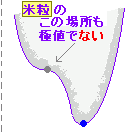 ���̐}�� y = |x| �� x = 0 �ɂ����Ĕ����W������`���ꂸ f’(x) = 0�ł͂���܂��C�������瑝���ɕω����Ă���̂ŁC�ɏ��ł��D 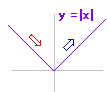 �@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@ ���@�v����ɁC�����C�������u�ω��v���Ă��邩�ǂ����Ŕ��f���܂��D�u�R�ɓ��H������Ƃ��v��u�܂�Ă���Ƃ���v�͗v���ӂƂ������Ƃł��D |