分数の指数（有理数の指数）

→ 携帯版は別頁 == 分数の指数（有理数の指数） == 【はじめに】分数（有理数）の指数が付いている式は累乗根で表される式と同じものです．多くの場合，分数の指数を使って計算する方が累乗根のまま計算するよりも簡単になります． ■分数（有理数）の指数の定義 a>0であってm, nが正の整数であるとき a=と定義します．特に a= a= 負の指数と組み合わせるときは，次のようになります． a−= a−= a−= （解説） ≪具体例で考える≫ (ax)y=axyという指数法則が自由に使えるようにしたい．たとえば，(ax)3=a5となるxを求めたいとき ○指数法則が成り立つようにするには (ax)3=a5→3x=5→x= すなわち， a という分数の指数を考える必要がある．このとき， (a)3=a5…(1) という計算を考えていることになる． ○他方で，累乗根について次の関係がある． ( )3=a5…(2) ○(1)(2)からa= と定義すればよいこと分かる． ≪一般に≫ 指数法則によれば (a)n=am 他方で，累乗根の定義によれば ( )n=am したがって a= (>0)と定義するとよい．	このページの「マイナーチェンジありカバー版」「パソコン用」ページ（グーグルブロガー版）は，こちら⇒ ○　数の種類と演算の関係　小学校では分数を習い，中学校では負の数，無理数（根号の付いた数）を習いましたが，このような数の種類の拡張は「割り算」や「引き算」のような演算の結果を表すために行われます．つまり，［数の種類→演算の考案］の順ではなく，［演算を自由に行う必要→数の種類の拡張］というように演算の結果を表す必要を優先的に考えて，これに応えられるように数の範囲を拡張したものです．例 5÷3という演算の結果を表したい→分数を考えた． 3−5という演算の結果を表したい→負の数−2を考えた． x2=3という方程式の解を表したい→無理数±を考えた． ○　（同様にして）指数の種類と演算の関係の考え方（中学校：指数が登場），（高校数学II：負の指数が登場），（高校数学II：分数の指数が登場）と広げていくのは指数法則を自由に行うために必要だからです．例 a3÷a5という演算の結果を表したい→負の指数a−2を考えた． (ax)3=a5となるxを表したい→分数の指数aを考える． ≪要点≫ 例 (1)8= 8=(23)=23×=22=4 ====4 (2)32= 32=(25)=25×=21=2 ==2 (3)9= 9=(32)=32×=31=3 ==3
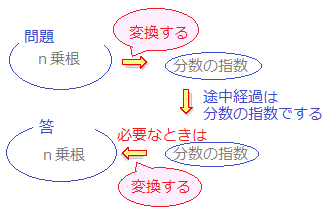
a, b>0であってp, qが有理数（分数または整数）のとき，次の計算法則が成り立つ． apaq=ap+q …(1) ap÷aq=ap−q …(2) (ap)q=apq …(3) (ab)p=apbp …(4) ()p= …(5)	例(2)，問題2(3)(4)，問題3(4)，問題4(2)～(5)のように問題が累乗根で書かれているときは，途中経過は分数の指数を使って行い，答を累乗根で書く必要があれば，結果を書き直すようにします．（累乗根のまま途中経過をやってしまうと計算が複雑になります．）
例次の式を簡単にしてください．結果は負の指数や有理指数を使わずに表してください． (a, b>0) (1)a×a− =a+(−)=a−=a = (2)÷ =(32)÷3 =3÷3=3−=3=3 = (3)(9−) =((32)−)=32×(−)×=3− =	(4)(ab−)−×(a−b)2 =a×(−)b−×(−)×a−×2b×2 =a−b×a−b =a−+(−)b+ =a−1b =

問題１a>0のとき，次の累乗根をaxの形で表しなさい．（正しいものを選びなさい。） (1) 解説 a a− a a−	=a
(2) 解説 a6 a−6 a a−	=a 一般に =aが成り立ちます
(3) 解説 a a− a a−	( )−1=(a)−1=a− 一般に =a−が成り立ちます．
(4) 解説 a2 a−2 a a−	( )−1=(a)−1=a− 一般に =a−が成り立ちます．
問題２次の式の値を求めなさい．（正しいものを選んでください．） (1) 4 解説 1 2 4 8 16 32	底を素因数分解すると (22)=23=8
(2) 16− 解説 1 2 4 8 16 32	底を素因数分解すると (24)−=2−3=
(3) 解説 1 2 4 8 16 32	底を素因数分解すると ((23)2)=23×2×=22=4
(4) 解説 1 2 4 8 16 32	底を素因数分解すると ((25)4)=25×4×=24=16
問題３次の式の値を求めなさい．（空欄を埋めてください．） (1) 3−×9×27= 採点するやり直す解説	底を素因数分解すると 3−×9×27 =3−×(32)×(33) =3−×3×3 =3−++ =3−++ =3 =31 =3
(2) 6−2×27÷12−= 採点するやり直す解説	底を素因数分解すると 6−2×27÷12− =(2×3)−2×(33)÷(22×3)− =(2−2×3−2)×3÷(2−3×3−) =2−2+33−2++ =2132 =18
(3) 24−1×18÷12−= 採点するやり直す解説	底を素因数分解すると 24−1×18÷12− =(23×3)−1×(2×32)÷(22×3)− =(2−3×3−1)×(2×3)÷(2−×3−) =2−3++3−1++ =2232=36
(4) = 採点するやり直す解説	有理指数に直すと =525 底を素因数分解すると =5(52) =55 =5+ =51 =5
問題４a, b>0のとき，次の式を簡単にしなさい．（正しいものを選んでください．） (1) (a)3×(a−)−1×a− 解説 1 a	(a)3×(a−)−1×a− =aaa− =a+− =a=a1=a
(2) ÷a 解説 1 a	累乗根を有理指数に直すと ÷a =(ab×a)÷ab =aba÷ab =a+−1b− =a− =
(3) 解説 1 a	累乗根を有理指数に直すと = ==1
(4) ÷ 解説 1 a	累乗根を有理指数に直すと ÷ =((a2))÷((a4)) =a2××÷a4×× =a− =a− =
(5) × 解説 1 a	累乗根を有理指数に直すと × =(a(a×a))×((a)) =(a×aa)×a =aaa×a =a++×a =a×a =a+ =a1 =a

Top menu

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数）について／18.7.18］

3分の２の6分の1乗を（2の6分の1乗×3の-6分の1乗）にするような例題もあってもいいかも。自分はこのサイトをみていたらひらめくことができましたが分数を分解することに気づかない人もいるはず
＝＞［作者］：連絡ありがとう．すべての材料を横に並べるのは，管理人おすすめの方法と一致します：なんでもかんでも $a^{\frac{q}{p}}b^{\frac{s}{r}}c^{\frac{u}{t}}\cdots$ に直す．

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数）について／18.3.21］

足し算も書いてほしい
＝＞［作者］：連絡ありがとう．質問の意味が不明です．指数の和になる場合については，そのページに初めから書いてあります． $a^pa^q=a^{p+ q}$ ．これに対して，本体の足し算 $a^p+ a^q$ のような計算？足したらよいのでは．

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数）について／18.3.5］

わかりやすかったです(≧▽≦) テスト勉強に利用させて頂きました!(^^)!
＝＞［作者］：連絡ありがとう．

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数）について／17.3.3］

むずかしい。
＝＞［作者］：連絡ありがとう．それ以前の内容がどれくらい身に付いているかによってハードルが超えられるかどうかに関係すると思います．

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数）について／17.2.24］

練習問題の解説欲しいです
＝＞［作者］：連絡ありがとう．あなたの学習の記録を見てみると，解説の箇所を読んだ形跡がありません．もしかして，問題を解いていないのではないでしょうか･･･解答をクリックすれば，画面上で採点でき，解説が出るようになっています．PDFなどで作られた読むだけの教材とは違い，応答型になっています．解答しなければ解説は出ません．

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数）について／17.2.23］

わかりやすかったです！
＝＞［作者］：連絡ありがとう．

■［個別の頁からの質問に対する回答］[分数の指数（有理数の指数)について／17.2.5］

問題４の（２）や例（４）など、掛けているのかそれとも指数なのか分かりにくいにので、スペースをもっと開けるか掛け算のマークを入れて欲しいです
＝＞［作者］：連絡ありがとう．ご指摘の点については了解できません．掛け算のマークを書き込む箇所はありません．