[II] 素因数分解を利用して共通な指数を探す方法
最大公約数,最小公倍数を求めるもう1つの方法は,素因数分解を利用する方法です.高校では通常この方法が用いられます.
○ 最大公約数を求めるには,
「共通な素因数に」「一番小さい指数」をつけます.
(解説)
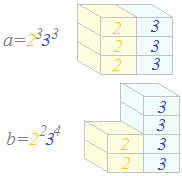 例えば,a=216, b=324の最大公約数を求めるには,
例えば,a=216, b=324の最大公約数を求めるには,
最初に,a, bを素因数分解して,
a=2333, b=2234
の形にします.
◇ 素因数2について,23と22の
「公約数」は,1, 2, 22
「最大公約数」は,22
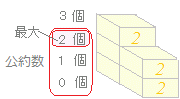
このように,公約数の中で最大のものは, 23と 22のうちの,小さい方の指数 2を付けたものになります!
「最大公約数」
⇒「共通な素因数に最小の指数」を付けます

◇ 同様にして,素因数3について,33と34の
「公約数」は,1, 3, 32, 33
「最大公約数」は,33
◇ 結局,a=2333, b=2234の最大公約数は2233=108

|
○ 最小公倍数を求めるには,
「全部の素因数に」「一番大きな指数」をつけます.
 (解説)
(解説)
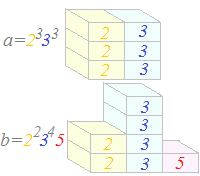
例えば,a=216, b=1620の最小公倍数を求めるには,
最初に,a, bを素因数分解して,
a=2333, b=22345
の形にします.
◇ 素因数2について,23と22の
「公倍数」は両方の倍数になっている数だから,23が入るものでなければなりません.
「公倍数」は23, 24, 25, 26, ...
「最小公倍数」は23
◇ 同様にして,素因数3について,33と34の
「公倍数」は,34, 35, 36, 37, ...
「最小公倍数」は,34
◇ ところが,素因数5については,aには入っていなくてbには入っています.この場合に,両方の倍数になるためには,5の倍数でなければなりません.
「公倍数」は5, 52, 53, ...
「最小公倍数」は5
◇ 結局,a=2333, b=22345の最小公倍数は23345=3240
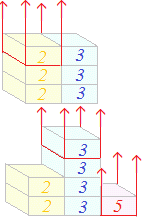
このように,公倍数の中で最小のものは,
◇ 23と 22のうちで大きい方の指数 3を付けたもの
◇ 33と 34のうちで大きい方の指数 4を付けたもの
◇素因数 5については,ないもの 50と1つあるもの 51のうちで大きい方の指数 1を付けたもの
となります.
⇒素因数 5の場合を考えてみると,「最小公倍数」を作るためには,「すべての素因数」を並べなければならないことがわかります.
「最小公倍数」⇒「すべての素因数に最大の指数」を付けます
|
|
【例題1】
a=75とb=315の最大公約数G,最小公倍数Lを求めてください.
(解答)
はじめに,a, bを素因数分解します.
a=3×52
b=32×5×7
最大公約数を求めるためには,「共通な素因数」3, 5に「最小の指数」1, 1を付けます.
G=31×51=15
最小公倍数を求めるためには,「すべての素因数」3, 5, 7に「最大の指数」2, 2, 1を付けます.
L=32×52×7=1575
【例題2】
a=72とb=294の最大公約数G,最小公倍数Lを求めてください.
(解答)
はじめに,a, bを素因数分解します.
a=23×32
b=21×31×72
最大公約数を求めるためには,「共通な素因数」2, 3に「最小の指数」1, 1を付けます.
G=21×31=6
最小公倍数を求めるためには,「すべての素因数」2, 3, 7に「最大の指数」3, 2, 2を付けます.
L=23×32×72=3528
|
【問題5】
2数 20, 98の最大公約数 Gと最小公倍数 Lを求めてください.
1G=2, L=490
2G=2, L=980
3G=4, L=49
4G=4, L=70
5G=4, L=490
HELP
はじめに,素因数分解します.
20=22×5
98=21×72
最大公約数を求めるためには,「共通な素因数」 2に「最小の指数」 1を付けます.
G=21=2
最小公倍数を求めるためには,「すべての素因数」 2, 5, 7に「最大の指数」 2, 1, 2を付けます.
L=22×51×72=980
→2
【問題6】
2数 a=22×33×52, b=22×32×7の最大公約数 Gと最小公倍数 Lを求めてください. (指数表示のままで答えてください)
1G=22×32, L=24×35
2G=22×33, L=24×35
3G=22×32, L=22×33×52×7
4G=22×32×52×7, L=24×35×52×7
HELP
最大公約数を求めるためには,「共通な素因数」 2, 3に「最小の指数」 2, 2を付けます.
G=22×32
最小公倍数を求めるためには,「すべての素因数」 2, 3, 5, 7に「最大の指数」 2, 3, 2, 1を付けます.
L=22×33×52×7
→3
|
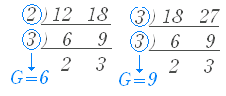
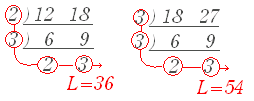

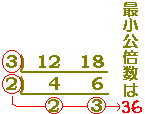
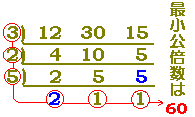
 例えば,
例えば, このように,公約数の中で最大のものは,
このように,公約数の中で最大のものは,

 (解説)
(解説) このように,公倍数の中で最小のものは,
このように,公倍数の中で最小のものは,