|
(Ⅰ) 具体的な値をx, yに代入してみて1つの解を見つけ,それを利用して一般解を求める方法 例えば
3x=4y(x, yは整数)…(2)
という問題では,右辺は4の倍数になっているが,左辺の3は4の倍数ではないからxが4の倍数でなければならない.x=4n(nは整数) このnを使って,元の方程式を書き直すと 12n=4y y=3n となって y=3n という一般解が得られる.具体的には次のような点になる.
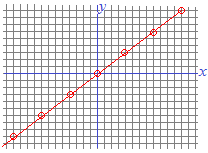
3(x−1)=4(y+2)(x, yは整数)…(3)
のような問題でも事情は同様であり,平行移動するだけで解ける.y+2=3n y=3n−2 右辺に定数項がある場合
3x−4y=5(x, yは整数)…(4)
のような問題では,具体的な値を幾つか代入してみて,1つの特別解を見つけると(3)の形に直して解くことができる.例えば,なんとか試行錯誤して 3×3−4×1=5…(4') という特別解を見つけると 3x−4y=5…(4)
−)3×3−4×1=5…(4')
3(x−3)−4(y−1)=03(x−3)=4(y−1) となって(3)の形の方程式に帰着させることができる. ※ただし,ax+by=cの形の不定方程式が常に解を持つとは限らない.例えば 6x+8y=5 のようにa, bが互いに素でない(最大公約数が1でない)場合,左辺が2の倍数であるのに右辺が2の倍数でないのだから,そのような整数解はない. また, 6x+8y=10 のように,3つの係数がいずれも2で割り切れる場合には,両辺を2で割って 3x+4y=5 の形に直して問題を解くものとすればよい.
【要約】
a, bが互いに素な整数であるとき, 1次方程式ax+by=c
を満たす整数解x, yを求めるには,1つの特別解x0, y0を見つけて,辺々引き算をすれば定数項を消去でき,次にa, bが互いに素という性質を使うと一般解が得られる.→右上に続く
|
【例題1】
(解答)1次方程式5x+3y=1 を満たす整数x, yの一般解を求めてください. x=2, y=−3は方程式を満たすから 5x+3y=1 −)5×2+3×(−3)=1
5(x−2)+3(y+3)=05(x−2)=−3(y+3) 左辺は5の倍数で,右辺の−3は5の倍数でないから,y+3が5の倍数でなければならない. y+3=5n y=5n−3(nは整数) このとき 5(x−2)=−15n x−2=−3n x=−3n+2 したがって y=5n−3
※初めに偶然見つけた解が,x=−1, y=2の場合は
5x+3y=1 −)5×(−1)+3×2=1
5(x+1)+3(y−2)=05(x+1)=−3(y−2) y=5m+2 となって見かけは異なるが,n, mがすべての整数をとるとき,これらが表すものは同じになる.原点がずれているだけである. (n=m+1になっている)
【例題2】
(解答)1次方程式3x+4y=30 を満たす正の整数x, yの組をすべて求めてください.
初めに整数の範囲で一般解を求めておき,
x=2, y=6は方程式を満たすから次にx>0, y>0の条件を満たすnの範囲を絞ります 3x+4y=30 −)3×2+4×6=30
3(x−2)+4(y−6)=03(x−2)=−4(y−6) y−6=3n y=3n+6(nは整数) このとき y=3n+6 次に,x, yは正の整数だから,x>0, y>0となるnの範囲を求める. x=−4n+2>0より nは整数だからn≦0 y=3n+6>0よりn>−2 nは整数だからn≧−1 以上から,n=−1, 0 (x, y)=(6, 3), (2, 6)…(答) |