|
�y��������̒�`�P�z
�ׂ荇���Q���̍������̒萔�ł��鐔������������Ƃ����܂�
�Q���̍��́C���̍�����O�̍������������̂Ƃ��܂�
��������������u�����v����ƍl����Ƃ悢 ��������ׂ̗荇���Q���̍��������Ƃ����܂�
�y��P�z
�i����j����1, 3, 5, 7,…… �͓�������ł��D �ׂ荇���Q���̍���  3−1=2
3−1=25−3=2 7−5=2 ……
�y��Q�z
�i����j����20, 17, 14, 11,…… �͓�������ł��D �ׂ荇���Q���̍���
17−20=−3
�Ƃ��ׂē����萔−3�ɂȂ��Ă��܂��D������−3�ł��D
14−17=−3 11−14=−3 ……
## �r�b�N������ ##
�@�ׂ荇��2���̍������̋K���Ő��藧���Ă��邾���ł́C��������Ƃ͌����܂���D �@��������ƌ����邽�߂ɂ́C�������́u�萔�v�C���Ȃ킿�u���̔ԍ��Ɉˑ����Ȃ��萔�v�Ƃ��āu�ǂ̂Q���Ԃɂ����ʂ̒萔�v�łȂ���Ȃ�܂���D �@�߂����ɂȂ����Ƃł����C  �E�̂悤�Ȑ�����u�����vn�̓������I�Ȃǂƍl���Ă͂����܂���D
�E�̂悤�Ȑ�����u�����vn�̓������I�Ȃǂƍl���Ă͂����܂���D�Q���Ԃ̍����u���̔ԍ�n�Ɉˑ����ĕω�����v�悤�Ȑ���͓�������Ƃ͌����܂���D |
��������́C�����i��P���j�Ɍ����ƂȂ�萔�����X�ɉ����Ă����Ɠ����܂��D�����ŁC�����̋��ȏ��ł́C������������̂悤�ɒ�`���Ă��܂��D
�y��������̒�`�Q�z
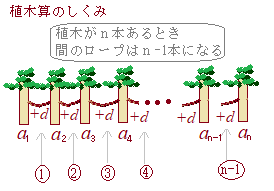
����a�ɒ萔d�����X�ɉ����ē����鐔������������Ƃ����C���̒萔d�������Ƃ����D
�y��P’ �z�i�Čf�j
�i����j����1, 3, 5, 7,…… �͓�������ł��D ����1�Ɍ���2�����X�ɉ����ē����鐔��ƂȂ��Ă��܂��D
1+2=3
3+2=5 5+2=7 ……
�y��Q’ �z�i�Čf�j
�i����j����20, 17, 14, 11,…… �͓�������ł��D ����20�Ɍ���−3�����X�ɉ����ē����鐔��ƂȂ��Ă��܂��D
20+(−3)=17
17+(−3)=14 14+(−3)=11 …… |
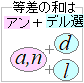 ���ǂ����
���ǂ����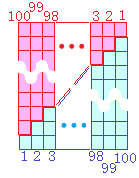
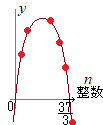 ����͏�ɓʁi�R�`�j�̂Q�����ɂȂ邩��C���_�ɍł��߂������l���ōő�ƂȂ�͂��ł���D
����͏�ɓʁi�R�`�j�̂Q�����ɂȂ邩��C���_�ɍł��߂������l���ōő�ƂȂ�͂��ł���D ������
������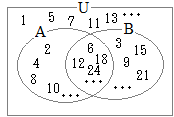 (3) �Q�ł��R�ł������Ȃ����́C1,5,7,9,11,...�ƂȂ��Ă��邩�瓙������ł͂Ȃ��D
(3) �Q�ł��R�ł������Ȃ����́C1,5,7,9,11,...�ƂȂ��Ă��邩�瓙������ł͂Ȃ��D