|
〇文字係数の2次不等式を解くときは,できるだけ「因数分解」を試みて,文字の値の大小によって場合分けして答えます.
【例1】
2次不等式x2−(a+2)x+2a<0を解いてください.
左辺を因数分解すると
右上に続く↑
|
(解答) ア) a<2のとき
ア) a<2のとき2次関数y=(x−2)(x−a)のグラフは右図のようになるから 2次不等式の解は a<x<2 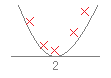 イ) a=2のとき
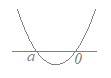
イ) a=2のとき2次関数y=(x−2)2のグラフは右図のようになるから 2次不等式は「解なし」 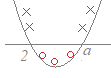 ウ) 2<aのとき
ウ) 2<aのとき2次関数y=(x−2)(x−a)のグラフは右図のようになるから 2次不等式の解は 2<x<a |
 ア)
ア) 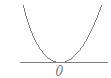 イ)
イ) 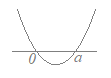 ウ)
ウ) 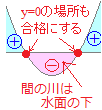 ア)
ア) 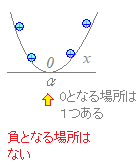 イ)
イ) 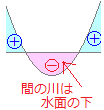 ア)
ア)  イ)
イ) 
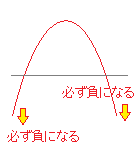
 上に凸のグラフだから
上に凸のグラフだから 下に凸のグラフだから,
下に凸のグラフだから, 右のグラフから分かるように,
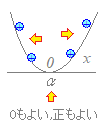
右のグラフから分かるように,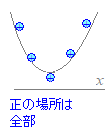
 イ)
イ)