== ベクトル内積(成分) ==
【例1】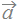 =(1 , 2 ) , =(1 , 2 ) ,  =(3 , 4 ) の内積は =(3 , 4 ) の内積は
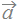 · · =1 · 3+2 · 4=11 =1 · 3+2 · 4=11
【例2】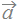 =(3 , 4 ) , =(3 , 4 ) ,  =(−5 , 7 ) の内積は =(−5 , 7 ) の内積は
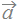 · · =3 · (−5)+4 · 7=13 =3 · (−5)+4 · 7=13
【例3】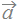 =(2 , −1 ) , =(2 , −1 ) ,  =(−3 , 0 ) の内積は =(−3 , 0 ) の内積は
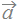 · · =2 · (−3)+(−1) · 0=−6 =2 · (−3)+(−1) · 0=−6
※ベクトルは2次元ですが、ベクトルの内積は単なる数になります。
3次元以上のベクトルでも同様にして、次のように成分x1, x2, …が与えられているとき、
| x1 |
x2 |
x3 |
x4 |
… |
| 2 |
-3 |
1 |
5 |
… |
| 4 |
-2 |
6 |
0 |
… |
2つのベクトルの内積は、2×4+(-3)×(-2)+1×6+5×0+…と定義されます。 ⇒ 積の和になります。
Excelのワークシート関数では = SumProduct(行1,行2) または= SumProduct(列1,列2)で内積が求められます。
※内積の計算に当たって「掛ける相手を間違わないこと」が重要。(x成分とx成分の積+y成分とy成分の積とします)
※ベクトルの内積は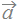 · · のように「ドット」で表すものとし、 のように「ドット」で表すものとし、
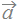 × × のように書いてはいけません。(×は「外積」と呼ばれる別のものを表します。) のように書いてはいけません。(×は「外積」と呼ばれる別のものを表します。)
|
 (参考)
(参考)
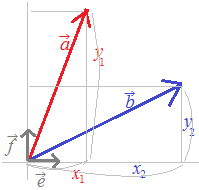
矢印で表されるベクトルについての内積の定義
 \( \vec{a}\cdot\vec{b}=\mid\vec{a}\mid\cdot\mid\vec{b}\mid\cos\theta \) \( \vec{a}\cdot\vec{b}=\mid\vec{a}\mid\cdot\mid\vec{b}\mid\cos\theta \)
から,成分で表されるベクトル
,\hspace{3}\vec{b}=(x_2,y_2)) \( \vec{a}=(x_1,y_1),\hspace{3px}\vec{b}=(x_2,y_2) \) \( \vec{a}=(x_1,y_1),\hspace{3px}\vec{b}=(x_2,y_2) \)
の内積の定義
 \( \vec{a}\cdot\vec{b}=x_1x_2+ y_1y_2 \) \( \vec{a}\cdot\vec{b}=x_1x_2+ y_1y_2 \)
を導く方法
ベクトルの内積については,次の分配法則が成り立ちます.これ自体は証明する必要がありますが,ここではこの結果を使って示す.
\vec{c}=\vec{a}\cdot\vec{c}%2B\vec{b}\cdot\vec{c}&chco=aa2200) \( (\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c} \) \( (\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c} \)
=\vec{a}\cdot\vec{c}%2B\vec{a}\cdot\vec{d}&chco=aa2200) \( \vec{a}\cdot(\vec{c}+\vec{d})=\vec{a}\cdot\vec{c}+\vec{a}\cdot\vec{d} \) \( \vec{a}\cdot(\vec{c}+\vec{d})=\vec{a}\cdot\vec{c}+\vec{a}\cdot\vec{d} \)
) \( \vec{e}=(1,0) \)とy軸の正の向きで大きさ1の基本ベクトル \( \vec{e}=(1,0) \)とy軸の正の向きで大きさ1の基本ベクトル) \( \vec{f}=(0,1) \)を用いて,ベクトル \( \vec{f}=(0,1) \)を用いて,ベクトル,\hspace{5}\vec{b}=(x_2,y_2)) \( \vec{a}=(x_1,y_1),\hspace{5px}\vec{b}=(x_2,y_2) \)は各々次のように表されます. \( \vec{a}=(x_1,y_1),\hspace{5px}\vec{b}=(x_2,y_2) \)は各々次のように表されます.
 \( \vec{a}=x_1\vec{e}+ y_1\vec{f} \) \( \vec{a}=x_1\vec{e}+ y_1\vec{f} \)
 \( \vec{b}=x_2\vec{e}+ y_2\vec{f} \) \( \vec{b}=x_2\vec{e}+ y_2\vec{f} \)
そこで,上に示した分配法則により
(x_2\vec{e}%2B y_2\vec{f})) \( \vec{a}\cdot\vec{b}=(x_1\vec{e}+ y_1\vec{f})\cdot(x_2\vec{e}+ y_2\vec{f}) \) \( \vec{a}\cdot\vec{b}=(x_1\vec{e}+ y_1\vec{f})\cdot(x_2\vec{e}+ y_2\vec{f}) \)
 \( =x_1x_2\vec{e}\cdot\vec{e}+ x_1y_2\vec{e}\cdot\vec{f}+y_1x_2\vec{e}\cdot\vec{f}+ y_1y_2\vec{f}\cdot\vec{f} \) \( =x_1x_2\vec{e}\cdot\vec{e}+ x_1y_2\vec{e}\cdot\vec{f}+y_1x_2\vec{e}\cdot\vec{f}+ y_1y_2\vec{f}\cdot\vec{f} \)
ところで基本ベクトル  \( \vec{e},\hspace{5px}\vec{f} \) \( \vec{e},\hspace{5px}\vec{f} \)の内積については,次の関係があります.
 \( \vec{e}\cdot\vec{e}=1\times 1\times\cos 0^{\circ}=1 \) \( \vec{e}\cdot\vec{e}=1\times 1\times\cos 0^{\circ}=1 \)
 \( \vec{f}\cdot\vec{f}=1\times 1\times\cos 0^{\circ}=1 \) \( \vec{f}\cdot\vec{f}=1\times 1\times\cos 0^{\circ}=1 \)
 \( \vec{e}\cdot\vec{f}=1\times 1\times\cos 90^{\circ}=0 \) \( \vec{e}\cdot\vec{f}=1\times 1\times\cos 90^{\circ}=0 \)
(同じものとの内積は1,異なるものとの内積は0になる)
したがって,
 \( \vec{a}\cdot\vec{b}=x_1x_2+ y_1y_2 \) \( \vec{a}\cdot\vec{b}=x_1x_2+ y_1y_2 \)
|
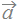 =(x1 , y1 ) ,
=(x1 , y1 ) ,  =(x2 , y2 ) の内積は
=(x2 , y2 ) の内積は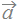 ·
· =x1x2+y1 y2
=x1x2+y1 y2
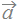 =(1 , 2 ) ,
=(1 , 2 ) ,  =(3 , 4 ) の内積は
=(3 , 4 ) の内積は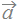 ·
· =1 · 3+2 · 4=11
=1 · 3+2 · 4=11
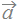 =(3 , 4 ) ,
=(3 , 4 ) ,  =(−5 , 7 ) の内積は
=(−5 , 7 ) の内積は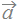 ·
· =3 · (−5)+4 · 7=13
=3 · (−5)+4 · 7=13
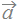 =(2 , −1 ) ,
=(2 , −1 ) ,  =(−3 , 0 ) の内積は
=(−3 , 0 ) の内積は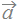 ·
· =2 · (−3)+(−1) · 0=−6
=2 · (−3)+(−1) · 0=−6
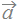 ·
· のように「ドット」で表すものとし、
のように「ドット」で表すものとし、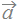 ×
× のように書いてはいけません。(×は「外積」と呼ばれる別のものを表します。)
のように書いてはいけません。(×は「外積」と呼ばれる別のものを表します。) (参考)
(参考)