== 数列の漸化式と極限 ==
【要点】
この頁では,漸化式で与えられた数列の極限について,次の3つの場合を学習します.
(I)一般項を求めることができ,求めた一般項から極限が求められる場合
【例】
 \( \displaystyle a_1=1,\hspace{10px}a_{n+ 1}=\frac{1}{2}a_n + 1 \) \( \displaystyle a_1=1,\hspace{10px}a_{n+ 1}=\frac{1}{2}a_n + 1 \)
から
^{n-1}) \( \displaystyle a_{n}=2-(\frac{1}{2})^{n-1} \) \( \displaystyle a_{n}=2-(\frac{1}{2})^{n-1} \)
が求まり,これにより
 \( \displaystyle \lim_{n \rightarrow \infty}a_{n}=2 \) \( \displaystyle \lim_{n \rightarrow \infty}a_{n}=2 \)
が示される → (ジャンプ)
(II)一般項を求めることはできないが,極限値の必要条件を絞り込むことができ,その極限値に収束することが証明できる場合
【例】
 \( \displaystyle a_1=1,\hspace{10px}a_{n+1}=\sqrt{a_n +2} \) \( \displaystyle a_1=1,\hspace{10px}a_{n+1}=\sqrt{a_n +2} \)
が極限値  \( \displaystyle \alpha \) \( \displaystyle \alpha \)を持つとすれば
 \( \displaystyle \alpha=2 \) \( \displaystyle \alpha=2 \)
が必要条件になる.次に十分条件を検討すると,
 \( \displaystyle \lim_{n \rightarrow \infty}| a_{n}-2 | =0 \) \( \displaystyle \lim_{n \rightarrow \infty}| a_{n}-2 | =0 \)
が満たされていることから
 \( \displaystyle \lim_{n \rightarrow \infty}a_{n}=2 \) \( \displaystyle \lim_{n \rightarrow \infty}a_{n}=2 \)
が示される → (ジャンプ)
(III)別の数列の極限との関係から問題の数列の極限が求まる場合
【例】
 \( \displaystyle \lim_{n \rightarrow \infty}\frac{a_{n} + 5}{2a_{n} + 1}=3 \) \( \displaystyle \lim_{n \rightarrow \infty}\frac{a_{n} + 5}{2a_{n} + 1}=3 \)
のとき
 \( \displaystyle \frac{a_{n} + 5}{2a_{n} +1}=b_n \) \( \displaystyle \frac{a_{n} + 5}{2a_{n} +1}=b_n \)
とおけば

 \( \displaystyle \lim_{n \rightarrow \infty}b_n =3 \) \( \displaystyle \lim_{n \rightarrow \infty}b_n =3 \)
 \( \displaystyle a_{n}=\frac{-b_n+ 5}{2b_n-1} \) \( \displaystyle a_{n}=\frac{-b_n+ 5}{2b_n-1} \)
から
 \( \displaystyle \lim_{n \rightarrow \infty}a_{n}=\frac{2}{5} \) \( \displaystyle \lim_{n \rightarrow \infty}a_{n}=\frac{2}{5} \)
が示される → (ジャンプ)
右上に続く↑
|
(I)の解説 *** 一般項を求めることができ,求めた一般項から極限が求められる場合
【例題 1.1】
次の条件によって定められる数列 { an} の極限を求めてください.
 \( \displaystyle a_1=1,\hspace{10px}a_{n+ 1}=\frac{1}{2}a_n +1 \) \( \displaystyle a_1=1,\hspace{10px}a_{n+ 1}=\frac{1}{2}a_n +1 \)
2項間漸化式
 \( \displaystyle a_{n+1}=pa_n +q \) \( \displaystyle a_{n+1}=pa_n +q \)
2項間の分数形の漸化式
 \( \displaystyle a_{n+ 1}=\frac{pa_n + q}{ra_n + s} \) \( \displaystyle a_{n+ 1}=\frac{pa_n + q}{ra_n + s} \)
3項間漸化式
 \( \displaystyle a_{n+ 2} + pa_{n+ 1}+ qa_n=0 \) \( \displaystyle a_{n+ 2} + pa_{n+ 1}+ qa_n=0 \)
については,一般項が求まる場合があります.このような場合には,一般項から極限を求めることができます.
) \( \displaystyle a_{n+ 1}-2=\frac{1}{2}(a_n -2) \)…(*) \( \displaystyle a_{n+ 1}-2=\frac{1}{2}(a_n -2) \)…(*)
と変形すると,数列 \( \displaystyle \{a_n -2\} \)は初項 \( \displaystyle \{a_n -2\} \)は初項  \( \displaystyle a_1 -2=-1 \),公比 \( \displaystyle a_1 -2=-1 \),公比 \( \displaystyle \frac{1}{2} \)の等比数列をなすから \( \displaystyle \frac{1}{2} \)の等比数列をなすから
\Bigl(\frac{1}{2}\Bigr)^{n-1}) \( \displaystyle a_{n}-2=(-1)\Bigl(\frac{1}{2}\Bigr)^{n-1} \) \( \displaystyle a_{n}-2=(-1)\Bigl(\frac{1}{2}\Bigr)^{n-1} \)
^{n-1}) \( \displaystyle a_{n}=2-\Bigl(\frac{1}{2}\Bigr)^{n-1} \) \( \displaystyle a_{n}=2-\Bigl(\frac{1}{2}\Bigr)^{n-1} \)
ゆえに
 \( \displaystyle \lim_{n\rightarrow \infty}a_{n}=2 \)…(答) \( \displaystyle \lim_{n\rightarrow \infty}a_{n}=2 \)…(答)
※
漸化式
 \( \displaystyle a_{n+ 1}=\frac{1}{2}a_n +1 \)…(1) \( \displaystyle a_{n+ 1}=\frac{1}{2}a_n +1 \)…(1)
に対して
 \( \displaystyle \alpha=\frac{1}{2}\alpha +1 \)を \( \displaystyle \alpha=\frac{1}{2}\alpha +1 \)を
特性方程式と言います.特性方程式の解(不動点) \( \displaystyle \alpha \)を用いると,漸化式(1)は \( \displaystyle \alpha \)を用いると,漸化式(1)は
) \( \displaystyle a_{n+ 1}-\alpha=\frac{1}{2}(a_n-\alpha) \) \( \displaystyle a_{n+ 1}-\alpha=\frac{1}{2}(a_n-\alpha) \)
と変形できます.(特性方程式については,この頁の下端に解説があります.)
なお,答案作成上は特性方程式にも不動点にも触れずに,上記の答案のように(なぜその変形を思いつくのかという理由を示さなくても,偶然思いついたかのようなふりをしながら)
 \( \displaystyle a_{n+1}=\frac{1}{2}a_n +1 \)を \( \displaystyle a_{n+1}=\frac{1}{2}a_n +1 \)を) \( \displaystyle a_{n+ 1}-2=\frac{1}{2}(a_n -2) \)に変形してもよい.(正しい変形であることは係数を比較すれば分かる) \( \displaystyle a_{n+ 1}-2=\frac{1}{2}(a_n -2) \)に変形してもよい.(正しい変形であることは係数を比較すれば分かる)
「特性方程式」はうまく使えばきれいに決まりますが,教科書には登場しません.「使える場面と使えない場面の違い」「αの意味」など自信が持てないときは次のような答案も可能です.
(別解)
もしそのような定数 αが存在したら,  \( \displaystyle \{a_n-\alpha\} \) \( \displaystyle \{a_n-\alpha\} \)が等比数列になってうれしいから,あれば求めるという立場に立つ
(存在しなければ,別の方法を試みるという腹つもりで)
) \( \displaystyle a_{n+ 1}-\alpha=\frac{1}{2}(a_n -\alpha) \)…(*) \( \displaystyle a_{n+ 1}-\alpha=\frac{1}{2}(a_n -\alpha) \)…(*)
となる定数 \( \displaystyle \alpha \)を求める. \( \displaystyle \alpha \)を求める.
 \( \displaystyle a_{n+1}=\frac{1}{2}a_n +1 \)…問題 \( \displaystyle a_{n+1}=\frac{1}{2}a_n +1 \)…問題
 \( \displaystyle a_{n+ 1}=\frac{1}{2}a_n + \frac{1}{2}\alpha \)…(*) \( \displaystyle a_{n+ 1}=\frac{1}{2}a_n + \frac{1}{2}\alpha \)…(*)
の係数を比較すると
 \( \displaystyle \alpha=2 \) \( \displaystyle \alpha=2 \)
そこで,
) \( \displaystyle a_{n+1}-2=\frac{1}{2}(a_n -2) \)が成り立つことになる. \( \displaystyle a_{n+1}-2=\frac{1}{2}(a_n -2) \)が成り立つことになる.
数列 \( \displaystyle \{a_n -2\} \)は初項 \( \displaystyle \{a_n -2\} \)は初項  \( \displaystyle a_1 -2=-1 \),公比 \( \displaystyle a_1 -2=-1 \),公比 \( \displaystyle \frac{1}{2} \)の等比数列をなすから \( \displaystyle \frac{1}{2} \)の等比数列をなすから
\Bigl(\frac{1}{2}\Bigr)^{n-1}) \( \displaystyle a_{n}-2=(-1)\Bigl(\frac{1}{2}\Bigr)^{n-1} \) \( \displaystyle a_{n}-2=(-1)\Bigl(\frac{1}{2}\Bigr)^{n-1} \)
^{n-1}) \( \displaystyle a_{n}=2-\Bigl(\frac{1}{2}\Bigr)^{n-1} \) \( \displaystyle a_{n}=2-\Bigl(\frac{1}{2}\Bigr)^{n-1} \)
ゆえに
 \( \displaystyle \lim_{n\rightarrow \infty}a_{n}=2 \)…(答) \( \displaystyle \lim_{n\rightarrow \infty}a_{n}=2 \)…(答)
|
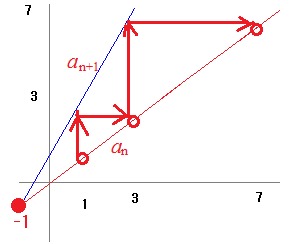 (失敗例2)
(失敗例2)