|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
難易度の目安 基 本:★☆☆
普 通:★★☆
やや難:★★★
|
|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
難易度の目安 基 本:★☆☆
普 通:★★☆
やや難:★★★
|
■必要条件・十分条件■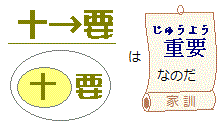 -- 図1 --
-- 図1 --
• 図で考えるときは,卵の黄身のように「中に入る小さい方を十分条件」,卵の白身のように「外側の大きい方を必要条件」という.  • pがqの必要条件であるか,十分条件であるかを判断するためには,「とにかくpとqの間に2つの矢印を書く」「どちら向きの矢印が成り立つかを調べる」
• pがqの必要条件であるか,十分条件であるかを判断するためには,「とにかくpとqの間に2つの矢印を書く」「どちら向きの矢印が成り立つかを調べる」(※図1の「十要は重要」の向きを見る事) 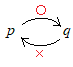 • 右図のように「p→q」が成り立ち,「q→p」が成り立たない場合は,「pはqの(pはqであるための)十分条件である」という.
• 右図のように「p→q」が成り立ち,「q→p」が成り立たない場合は,「pはqの(pはqであるための)十分条件である」という.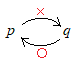 • 右図のように「q→p」が成り立ち,「p→q」が成り立たない場合は,「pはqの(pはqであるための)必要条件である」という.
• 右図のように「q→p」が成り立ち,「p→q」が成り立たない場合は,「pはqの(pはqであるための)必要条件である」という.• 両方とも成り立つ場合は「必要十分条件」,どちらも成り立たない場合は「必要条件でも十分条件でもない」という. |
|
【問題1】★☆☆
[解説を読む]条件「x4=1」は条件「x=1」の必要条件か,十分条件か,必要十分条件か,あるいはそのいずれでもないか,答えなさい. (2000年度名古屋学院大 経済学部)
x4=1 ⇔ (x2+1)(x+1)(x−1)=0 ⇔ x=±i, −1, 1
であるから 「x4=1」 x4=1のとき,x=1とは限らず,x=−1の場合やx=±iの場合もあり得るから 代入すれば成り立つのは明らかだから |
|
【問題2】★☆☆
[解説を読む]つぎの1から6の文中の空欄にあてはまるものを後述の選択肢(1)~(4)のうちから1つ選び,番号で答えなさい.文中x, yはともに実数とする. 1. 「x>0」は「x≧0」のための. 2. 「x=0」は「x2+y2=0」のための. 3. 「xy=0」は「x=0かつy=0」のための. 4. 「x2+y2=1」は「x+y=0」のための. 5. 「すべてのxについてxy=0である」は「y=0」のための. 6. 「(xy)2が無理数である」は「xまたはyが無理数である」のための. [選択肢]
(1) 必要十分条件である
(2) 十分条件であるが必要条件ではない (3) 必要条件であるが十分条件ではない (4) 必要条件でも十分条件でもない (2009年度慶應義塾大 環境情報学部)
1. → (2)
「x>0」ならば「x≧0」は,成り立つ
2. → (3)「x≧0」ならば「x>0」は,x=0のとき成り立たない よって,x>0
「x=0」ならば「x2+y2=0」は,成り立たない.
3. → (3)
∵y≠0のとき,x2+y2>0になる
「x2+y2=0」ならば「x=y=0」となるから,x=0は成り立つよって, x=0
「xy=0」ならば「x=0かつy=0」は,成り立たない.
4. → (4)
∵x=0, y=1のとき,「xy=0」であるが「x=0かつy=0」にはならない
「x=0かつy=0」ならば「xy=0」は成り立つよって, xy=0
「x2+y2=1」ならば「x+y=0」は,成り立たない.
5. → (1)
∵x=0, y=1のとき,「x2+y2=1」であるが「x+y=0」にはならない
「x+y=0」ならば「x2+y2=1」は,成り立たない.
∵x=0, y=0のとき,「x+y=0」であるが「x2+y2=1」にはならない
よって,x2+y2=1
「すべてのxについてxy=0である」ならば「y=0」は,成り立つ.
6. → (2)
∵「すべてのxについてxy=0である」のとき,例えばx=1のときもxy=0になるはずだから,「y=0」が成り立つ
「y=0」ならば「すべてのxについてxy=0である」は,成り立つ.よって,すべてのxについてxy=0である
「(xy)2が無理数である」ならば「xまたはyが無理数である」は,成り立つ.
∵「xもyも有理数である」ならば「(xy)2は有理数である」から,その対偶によって示される
「xまたはyが無理数である」ならば「(xy)2が無理数である」は,成り立たない.
∵
よって,「(xy)2が無理数である」 |
|
【問題3】★☆☆
[解説を読む]x, yが実数であるとき,次の文中の空欄に当てはまるものを,下の1, 2, 3, 4から1つ選べ. (ⅰ)
「x+y>0かつxy>0」は,「x>0かつy>0」であるためのア.
(ⅱ)
「x+y>2またはx+y<−2」は,「x>1かつy>1」であるためのイ.
(ⅲ)
「|x|<1かつ|y|<1」は,「xy+1>x+y」であるためのウ.
(ⅳ)
「y≦x2」は,「y≦x」であるためのエ.
(ⅴ)
「x2+y2<2」は,「|x|+|y|<2」であるためのオ.
1. 必要十分条件である
2. 必要条件であるが,十分条件ではない 3. 十分条件であるが,必要条件ではない 4. 必要条件でも十分条件でもない (2011年度成蹊大 経済学部)
(ⅰ) の解は1. すなわち,次の通り
「x+y>0かつxy>0」 xy>0より「x>0かつy>0」・・・(*1)または「x<0かつy<0」・・・(*2) 次に,x+y>0により,(*1)が成り立ち(*2)は成り立たない. (ⅱ)の解は2. すなわち,次の通り 「x+y>2またはx+y<−2」 x=−2かつy=−3のとき,x+y<−2が成り立つから,「x+y>2またはx+y<−2」が成り立つ.しかし,「x>1かつy>1」は成り立たない. (ⅲ)の解は3. すなわち,次の通り 「|x|<1かつ|y|<1」(A) 「xy+1>x+y」⇔「(x−1)(y−1)>0」 ⇔「(x−1)>0かつ(y−1)>0」または「(x−1)<0かつ(y−1)<0」 ⇔「x>1かつy>1」または「x<1かつy<1」 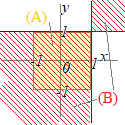 右図のように,(A)の領域⊂(B)の領域だから,(A)
右図のように,(A)の領域⊂(B)の領域だから,(A)となる (ⅳ)の解は4. すなわち,次の通り  「y≦x2」
「y≦x2」• 例えば,「y≦x2」を満たす点x=−1, y=0は,「y≦x」を満たさないから, • 例えば,「y≦x」を満たす点x=0.5, y=0.5は,「y≦x2」を満たさないから,  (ⅴ)の解は3. すなわち,次の通り
(ⅴ)の解は3. すなわち,次の通り「x2+y2<2」 • x2+y2=2の半径は • ±x±y=2と原点との距離は |
|
【問題4】★☆☆
[解説を読む]実数aに関する条件p, q, rを次のように定める.
p : a2≧2a+8
(1) 次のクに当てはまるものを,下の⓪~③のうちから一つ選べ.q : a≦−2またはa≧4 r : a≧5
pはqであるためのク.
⓪ 必要十分条件である
(2) 条件qの否定をq,条件rの否定をrで表す.① 必要条件であるが,十分条件でない ② 十分条件であるが、必要条件でない ③ 必要条件でも十分条件でもない 次のケ,コに当てはまるものを,下の⓪~③のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい.
命題「pならばケ」は真である.
命題「コならばp」は真である.
⓪ qかつr ① qまたはr
② qかつr ③ qまたはr (2009年度センター試験)
(1)
ク←⓪
p : a2≧2a+8 ⇔ a2−2a−8≧0
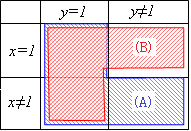
(2)⇔ (a−4)(a+2)≧0 ⇔ a≦−2, 4≦a : q 以上により,pはqであるための必要十分条件⓪ ク←① 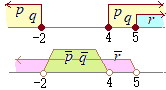 命題p, q, r, p, q, rに対応する集合を各々P, Q, R, P, Q, Rで表して,図示すると右図のようになる
命題p, q, r, p, q, rに対応する集合を各々P, Q, R, P, Q, Rで表して,図示すると右図のようになる P⊂(Q∪R)
P⊂(Q∪R)が成り立つ P⊃(Q∪R) が成り立つ 与えられた集合の中で,他に集合Pとの包含関係が決まる集合はない |
|
【問題5】★☆☆
[解説を読む]自然数nを自然数mで割った余りr ( 0≦r<m※ )を n mod mと書く.x, yは0以上の整数として,つぎの8つの条件のそれぞれが x mod 2=y mod 2 の必要十分条件であるかどうかを判定せよ.もし,必要十分条件なら1を,そうでなれけば0を対応する解答欄にマークしなさい. 1. x+yは奇数である.
2. x+yは偶数である.
3. xyは奇数である.
4. xyは偶数である.
5. 3x+7yは偶数である.
6. (x+1)y2は奇数である.
7. x+yおよびはxyはともに偶数である.
8. xyは4で割り切れない偶数である.
(2009年度慶應義塾大 総合政策学部)
上記の※印の部分は,原文を訂正した結果
x mod 2=y mod 2とは,「x, yが"偶数と偶数"か"奇数と奇数"の組になる」ということだから
1. → 0
「x+yは奇数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」ではない
2. → 1※逆の真偽も調べてもよいが,この段階で,必要十分ではない→0は言える
「x+yは偶数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立つ
3. → 0
∵対偶:「x, yが"偶数と奇数"の組」ならば「x+yは奇数である」が真だから
「x, yが"偶数と偶数"か"奇数と奇数"の組」ならば「x+yは偶数である」は成り立つ以上により,「x+yは偶数である」
「xyは奇数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立つ
4. → 0
∵実際には,奇数と奇数の組になっている
「x, yが"偶数と偶数"か"奇数と奇数"の組」ならば「xyは奇数である」は成り立たない
∵偶数と偶数の組のとき,xyは奇数にならない
以上により,「xyは奇数である」
「xyは偶数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立たない
5. → 1
∵奇数と偶数の組でも,xyは偶数になるから
※逆の真偽も調べてもよいが,この段階で,必要十分ではない→0は言える
「3x+7yは偶数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立つ
6. → 0
∵x, yが奇数と偶数の組のとき,3x, 7yは奇数と偶数になるから,3x+7yは奇数になる.よって,対偶によって示される.
「x, yが"偶数と偶数"か"奇数と奇数"の組」ならば「3x+7yは偶数である」は成り立つ
∵x, yが"偶数と偶数"のときは,3x+7yは偶数になる.
以上により,「3x+7yは偶数である」x, yが"奇数と奇数"のときも,3x+7yは偶数になる.
「(x+1)y2は奇数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立たない
7. → 0
∵「(x+1)y2は奇数である」ならば「x+1, yが奇数」,したがって「xが偶数,yが奇数」
※逆の真偽も調べてもよいが,この段階で,必要十分ではない→0は言える
「x+yおよびxyはともに偶数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立つ
8. → 0
∵「x+yおよびxyはともに偶数である」ならば「x, yとも偶数」,したがって,「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立つ
「x, yが"偶数と偶数"か"奇数と奇数"の組」ならば「x+yおよびxyはともに偶数である」は成り立たない
∵「x, yがともに奇数である」ならば「xyは奇数になる」
以上により,「x+yおよびxyはともに偶数である」
「xyは4で割り切れない偶数である」ならば「x, yが"偶数と偶数"か"奇数と奇数"の組」は成り立たない
∵x=1, y=2のとき,「xyは4で割り切れない偶数である」であるが「x, yが"偶数と偶数"か"奇数と奇数"の組」になっていない
※逆の真偽も調べてもよいが,この段階で,必要十分ではない→0は言える |
|
【問題6】★☆☆
[解説を読む]a, bを有理数とする.次の命題(1), (2)はそれぞれ「a+bが整数である」ための
「必要条件であるが,十分条件でない」,
のいずれであるかを述べ証明せよ.「十分条件であるが,必要条件でない」, 「必要十分条件である」, 「必要条件でも十分条件でもない」 (1) 「a, bはともに整数である」 (2) (1)または「a, bはいずれも整数ではない」 (2000年度山口大)
(1)
「a, bはともに整数である」ならば「a+bが整数である」は真 「a+bが整数である」ならば「a, bはともに整数である」は偽
反例:a=0.3, b=0.7のとき,「a+bが整数である」が「a, bはともに整数である」と言えない
「十分条件であるが,必要条件でない」・・・(答)(2) 「『a, bはともに整数である』または『a, bはいずれも整数ではない』」ならば「a+bが整数である」は偽
反例:a=0.1, b=0.2のとき,『a, bはいずれも整数ではない』が「a+bが整数である」と言えない
「a+bが整数である」ならば「『a, bはともに整数である』または『a, bはいずれも整数ではない』」は真
a+b=n(nは整数)のとき,
「必要条件であるが,十分条件でない」・・・(答)
aが整数であるならば,b=n−aも整数になる.
以上のように,「a+bが整数である」ならば「『a, bともに整数である』または『a, bはいずれも整数ではない』」
bが整数であるならば,a=n−bも整数になる. aが整数でないならば,b=n−aも整数でない. bが整数でないならば,a=n−bも整数でない. |
|
【問題7】★★☆
[解説を読む]実数x, yに対して,「x=1でないかまたはy=1」は(x−1)(y−1)=0であるための(ⅳ). (a) 必要十分条件である (b) 十分条件だが必要条件ではない (c) 必要条件だが十分条件ではない (d) 必要条件でも十分条件でもない (2011年度北見工業大)
 「x=1でないかまたはy=1」
「x=1でないかまたはy=1」⇔「x≠1またはy=1」(A) (x−1)(y−1)=0 ⇔「x=1またはy=1」(B) とすると(A)(B)のいずれも他方の部分集合でない. • 例えば,x=2, y=3は(A)を満たすが(B)を満たさない. したがって,(A)は(B)の十分条件ではない • 例えば,x=1, y=2は(B)を満たすが(A)を満たさない. したがって,(A)は(B)の必要条件ではない (d)必要条件でも十分条件でもない・・・(答) |
|
【問題8】★★☆
[解説を読む](3) 有限集合Aの要素の個数をn(A)と表すことにする. 2つの集合A, Bについて
• n(A∪B)≦n(A)は,A∪B=Øであるためのケ
ただし,ケ,コ,サ,シには,次の選択肢の中から適切なものを選び,その記号(ⅰ),(ⅱ),(ⅲ),(ⅳ)のいずれかを書け.• n(A)+n(B)≦n(A∩B)は,n(A∪B)=Øであるためのコ • n(A∪B)≦n(A)は,A⊂Bであるためのサ • n(A∪B)≦n(A∩B)は,A⊂Bであるためのシ
(ⅰ) 必要条件であるが十分条件ではない.
(ⅱ) 十分条件であるが必要条件ではない. (ⅲ) 必要十分条件である. (ⅳ) 必要条件でも十分条件でもない. (2021年度神奈川工科大)
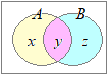 集合の要素の個数を右図のようにx, y, zで表すことにする.(以下の問題でも同様)
集合の要素の個数を右図のようにx, y, zで表すことにする.(以下の問題でも同様)ただし,x, y, zには重複はなく,例えばn(A)=x+y, n(B)=y+zとなる. また,x, y, z≧0だから,例えばx+y≦0ならばx=y=0が言える ケ←(ⅰ)
n(A∪B)≦n(A)ならば
コ←(ⅲ)
x+y+z≦x+y → y+z≦0 → y=z=0 → B=Ø
A∪B=Øならば
x+y+z=0 → x=y=z=0
以上から,n(A∪B)≦n(A)となるから,必要条件(ⅰ)
n(A)+n(B)≦n(A∩B)ならば
サ←(ⅳ)
(x+y)+(y+z)≦y → x+y+z≦0 → x=y=z=0
n(A∪B)=Øならば
x+y+z=0 → x=y=z=0
以上から,n(A)+n(B)≦n(A∩B) となるから,必要十分条件(ⅲ)
n(A∪B)≦n(A)ならば
シ←(ⅱ)
x+y+z≦x+y → z≦0 → z=0
A⊂Bならば
※正しくはA⊃Bになる
x=0
以上から,n(A∪B)≦n(A) となるから,必要条件でも十分条件でもない(ⅳ)
n(A∪B)≦n(A∩B)ならば
x+y+z≦y → x+z≦0 → x=z=0
A⊂Bならば
x=0
以上から,n(A∪B)≦n(A∩B)※すなわちy+z≦yとはならない
となるから,十分条件(ⅱ) |
|
【問題9】★★☆
[解説を読む]rは正の定数とする.実数x, yに関する条件p, qを次で定める.
p : −5≦x+y≦5かつ−5≦x−y≦5
(ⅰ) 「pはqであるための必要条件である」ような正の定数rの範囲はオである.q : x2+y2−2x−4y+5≦r2 (ⅱ) 「pはqであるための十分条件である」ような正の定数rの範囲はカである. (2021年度東海大学 医学部)
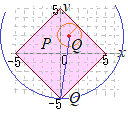 pは,右図の桃色で示した範囲Pに対応する(境界線を含む)
pは,右図の桃色で示した範囲Pに対応する(境界線を含む)qは,(x−1)2+(y−2)2≦r2と変形できるから,点(1, 2)を中心とする半径rの円の内部及び周上Qに対応する Q⊂Pとなるためにはrは点(1, 2)と直線x+y=5の間の距離 以下であればよい.オ← P⊂Qとなるためにはrは点(1, 2)と点(0, −5)の間の距離 以上であればよい.カ← (なお,点(1, 2)と点(−5, 0)の間の距離 |
|
【問題10】★★★
[解説を読む]a, b, cを定数とし,a≠0とする.条件p, q, r, s, tを次のように定める.
p:
方程式ax2+bx+c=0は異なる2つの実数解をもつ
このとき,qはpのケ.rはqのコ.sはpのサ.tはqのシ.q: 座標平面で関数y=ax2+bx+cのグラフはx軸と異なる2点で交わる r:ac<0である s:b2−ac>0である t:(a+b+c)(a−b+c)<0である ①必要十分条件である②必要条件であるが,十分条件でない ③十分条件であるが,必要条件でない④必要条件でも十分条件でもない (2014年度金沢工業大)
ケ←①
a≠0のとき,D=b2−4ac>0とp, qが同値であることは,教科書レベルの基本です
コ←③
a≠0のとき
サ←②
ac<0→D=b2−4ac>0
は言えるが
D=b2−4ac>0→ac<0
は必ずしも成り立たない.例えば,a=1, b=1, c=0のとき,D=b2−4ac>0であるがac<0ではない.以上から,rはqの十分条件
a≠0のとき
ア) ac>0ならば
よって,「qならばsは成り立つ.」D=b2−4ac>0 ⇔ b2>4ac>acだからb2>acが成り立つ イ) ac<0ならば D=b2−4ac>0の符号が正負のいずれであってもb2>acが成り立つ ウ) ac=0ならば D=b2−4ac>0 ⇔ b2>4ac=acだからb2>acが成り立つ 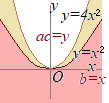
※右図のように,b=x, ac=y, 4ac=yのグラフで考えてもよい
逆に,a≠0のとき
シ←③
b2>acでもb2>4ac>0が成り立つとは限らない
例えば,b=2, a=1, c=1のとき,b2−ac=3>0であるがb2−4ac>0ではない. 以上から,sならばrは成り立たない
f(x)=ax2+bx+cとおくと
条件tは,f(1)f(−1)<0を表している.すなわち,y=f(x)のグラフは,x=1とx=−1の間でx軸と交わる.
したがって,「tならばqは成り立つ」 逆に,「qならばtは必ずしも成り立たない」 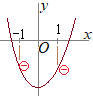
右図のように,f(1)とf(−1)が同符号であっても,D=b2−4ac>0となることがある. 例えば,a=1, b=0, c=−4のとき,b2−4ac>0であるがf(1)f(−1)<0ではない. |
|
下記のリンクを使ってメニューに戻ってください. |