|
■[個別の頁からの質問に対する回答][展開公式1について/18.9.4]
(4) (x+1)(x2−2x+1) この問題 すごい 公式がちがちだったのでまんまと間違えました
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/18.8.31]
分かりやすく、いつも利用しています。全国的な大まかな学習の順番をならべてくれると助かります
=>[作者]:連絡ありがとう. メニューの目次が,ほぼ教科書の目次の順です.教科書の目次は会社によって順序が変わるところがある.
65才になり約50年ぶりに高校数学に(再)挑戦してみました。実に分かりやすく楽しめました。有難うございます。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式について/18.6.14]
こういうサイトを作っていただきありがとうございます。
=>[作者]:連絡ありがとう.教科書レベルの基本にニーズがあるという意味に理解しました.
■[個別の頁からの質問に対する回答][展開公式1について/18.5.24]
だいぶ忘れてしまっていた。な、4つしか正解していないだと。そうだよなぁ。14年前に習ったものだもの。ただの暇つぶしですよ。教材としては最高に良い出来だと思います。
by もうじき三十路の孤独なおじさん
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/18.5.3]
(Xの三乗➖Yの三乗)(Xの三乗➕Yの三乗)
の簡単な因数分解の仕方・正しい因数分解の仕方を教えてください
=>[作者]:連絡ありがとう.因数分解のことは 因数分解のページを見てください.
56歳です。ボケ防止のために(ややボケが入っていますが)始めました。
今回はクリアできましたが、以後壁にぶち当たることが多々出てくると思います。よろしくお願いします。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/18.1.16]
とてもわかりやすく見やすかったです。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/18.1.15]
学校の授業が嫌になったので、ここに来ました。正直に言うと、授業よりわかりやすい。
これからテスト勉強とかここでしよう。
=>[作者]:連絡ありがとう.授業や教科書は必要最小限のことが詰まっていて,能率がよいので大事にする方がよい.こちらの教材も使えるところは使ってください.
■[個別の頁からの質問に対する回答][展開公式1について/18.1.6]
わかりやすい、そして問題も引っ掛けとかあっていい。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/17.12.03]
すごくいいとは思うのですが、どれを選んだかわかるようにしていただけるとなお助かると感じました。
=>[作者]:連絡ありがとう.その方が分かり易いと思うことで,直せるものは直すという考え方で,直しました.
■[個別の頁からの質問に対する回答][展開公式1について/17.11.26]
分かりやすく理解できました。ありがとうございます。
[Ⅶ][Ⅸ]の見分けるのを早く出来るのには練習しかないでしょうか?コツがあれば教えて頂きたいです。
=>[作者]:連絡ありがとう.[Ⅶ]と[Ⅸ]は全く違うものです.ゆっくり見れば分かります.
■[個別の頁からの質問に対する回答][展開公式1について/17.11.24]
問の正誤がすぐわかるので便利です。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][ 展開公式について/17.8.16]
詳しくて練習もついてる。たいへん助かりました。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/17.8.15]
公式が目の前にあると、計算しやすい!
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/17.8.15]
公式を自分で導き出せるようになった!
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/17.8.15]
回答が事前に書いてあり、自分の回答に自信のない時、回答の導き方が思い出せる!
=>[作者]:連絡ありがとう.数学のことでなく漢字のことですが,問題の答えは解答,返事は回答と書くのが普通です.
■[個別の頁からの質問に対する回答][展開公式1について/17.5.29]
とてもわかりやすく、4択で問題数も少ないので気軽にとりくむことができました。ありがとうございました。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/17.4.16]
問題3の(3)、(x+2)(x2-2x+4)ついてなのですが、xの係数は2ではないですか?
公式はどうして使えるのでしょうか
=>[作者]:連絡ありがとう.よく似た質問が時々あります.次の点に注意して下さい.
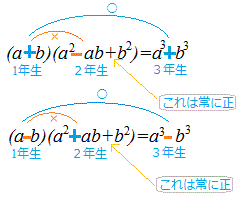
公式Ⅷ (a+b)(a2−ab+b2)=a3+b3 において,「abの係数が2のときはこの公式は使えない」
すなわち,(a+b)(a2−2ab+b2)はa3+b3にはならないと書いてあります.
しかし,問題3の(3)は,この公式でa=x, b=2としたものなので,
(x+2)(x2−2x+22)=x3+23 となっているのです.
一言でいえば,係数が2なのでなく,bが2なのです.
だから公式Ⅷが使えるのです.
1番最後の問題。なぜXの係数が-2だと公式が使えないのかわかない!!その他使えないときの例はありますか??
=>[作者]:連絡ありがとう.公式に合わなければ公式が使えないのは当然だと思いますが.
(a+b)(a2−ab+b2)=a3+b3:公式
→公式に合う(x+1)(x2−x+12)=x3+13
→公式に合わない(x+2)(x2−x+12):展開してみないと分からない
→公式に合わない(x+1)(x2+12):展開してみないと分からない
→公式に合わない(x+1)(x2−2x+12):展開してみないと分からない
→公式に合わない(x+1)(x2−3x+12):展開してみないと分からない
(a−b)(a2+ab+b2)=a3−b3:公式
→公式に合う(x−1)(x2+x+12)=x3−13
→公式に合わない(x−1)(x2+12):展開してみないと分からない
→公式に合わない(x−1)(x2+2x+12):展開してみないと分からない
→公式に合わない(x−1)(x2+3x+12):展開してみないと分からない
→公式に合わない(x−1)(x2+4x+12):展開してみないと分からない
公式を使える問題なのか使えない問題なのかがよく分かりません
=>[作者]:連絡ありがとう.係数も含めて同じ形になっているかどうかで判断します.その頁は公式が使える問題と使えない問題を見分ける練習にもなっていますので「分からない」というのは勉強不十分ということです.
あなたの目の動きをたどってみると,3乗の展開公式のところを何度も見ています.確かに公式[VI]~[IX]があなたの弱い箇所なのでそこをもう一度よく読んでみるとよいでしょう.
■[個別の頁からの質問に対する回答][展開公式1について/17.3.17]
[VIII][IX]の例の説明で,二段目の数式のが(見たらすぐ答え。特別な計算はいらない)理由がわからない。abの係数は2なので気長にばらばらにする必要があるのではないか.
=>[作者]:連絡ありがとう.{(2x)−1}{(2x)2+(2x)+1}の係数は全部1になっています(ただし最初のかっこ内の定数は−1です).
■[個別の頁からの質問に対する回答][展開公式について/17.3.11]
とてもわかりやすかったです
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/17.3.8]
最後はずるいw
=>[作者]:連絡ありがとう.この間違いは結構多いので,注意を促すためにあえて出題しています.
■[個別の頁からの質問に対する回答][展開公式について/17.1.16]
全て素晴らしい
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式について/16.12.27]
41のおっさんです。小さい頃から母親から罵られまくって高校に入って全く自暴自棄になって、勉強しなかったのですが、今落ち着いて見直すととても面白いです。欲を言えば、誘惑になる広告が非表示だといいですね。これからも使わせてもらいます。素晴らしいサイトをつくってくれてありがとう。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1について/16.12.21]
問題3の(4)、公式から外れたものを出題しているのがとても良いと思いました
=>[作者]:連絡ありがとう.何でも公式にあてはまると考えられると,とんでもない答案ができてしまうので,注意を促すために入れました.
■[個別の頁からの質問に対する回答][展開公式について/16.12.17]
合っていたら記号を『×→○』にしてほしい。
=>[作者]:連絡ありがとう.SafariかChromeで全角数字で入力していませんか?今の生徒は小学校以来コンピュータを使う授業を経験しているので,漢字の一種の全角文字(2バイト文字)と半角英数字(1バイト文字)の違いは分かっているはずです.数値計算は半角数字で行います.…(A)
とはいっても,現代生活は忙しいので,半角文字を入れるべき時に間違って全角文字を入力している場合に,コンピュータが勝手に訂正して半角文字に書き換えてしまうこともあります(Excelなど).…(B)
その頁では(A)の方式で採点しています…全角数字で答えると不正解になります.(ime-modeを無効にする設定を行っているので,ブラウザによっては全角入力を防げますが,あなたのブラウザでは全角入力ができてしまうようです)
■[個別の頁からの質問に対する回答][展開公式について/16.11.16]
全体的に、フォントの色が淡かったり、線が細かったりして少々読みづらい
=>[作者]:連絡ありがとう.文字色は少し濃くしました.Chromeで線が細く見えるとはどういうことなのか分かりません.
|