|
このページのマイナーチェンジありカバー版ページ
(グーグルブロガー版)は,こちら⇒ ■三角比の相互関係 《解説》
○ 高校数学Iで登場する「三角比の相互関係」とは、次の2つの公式のことです。
sin2A+cos2A=1 …(1) tanA = …(2) 三角比sinA , cosA , tanAのうち1つ分かれば、残りはこれらの公式を使って「芋づる式に」求まります。 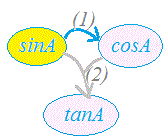 ○ 例えば、sinAが分かれば(1)を使ってcosAが求まり、さらに(2)を使ってtanAが求まります。 ○ 例えば、sinAが分かれば(1)を使ってcosAが求まり、さらに(2)を使ってtanAが求まります。しかし、例えばtanA = のように、三角比のうちでtanAだけが与えられて残りのsinA , cosAを求めるときは要注意です。 (2)からsinA=3 , cosA=4などと間違う生徒が多いからです。(−1≦sinA , cosA≦1を満たしていないので、間違いに気づくはずです。比だけが与えられているのだから、3/2:4/2 あるいは3/5:4/5の可能性も考えなければなりません。) このように、tanA ⇒ cosA(またはsinA)の関係式が必要なときは、(1)の両辺をcos2A(またはsin2A)で割って次の公式(3)(4)を「その場で作ればよい」。(「公式」を覚えるのでなく、必要になったときに作るようにします・・・「公式がある」ということだけを覚えておく…覚えなければならない公式の数を減らして、公式間の関連をつかむようにする)
tan2A+1 = …(3)
1+ = …(4) 例1
sinA = (0°≦A≦180°)のときcosAの値を求めてください。
(答案)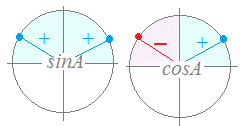 sin2A+cos2A=1にsinA = を代入すると
sin2A+cos2A=1にsinA = を代入すると( )2+cos2A=1 cos2A=1−= cosA=± 右図のようにsinA = のとき、Aは第1象限の場合も第2象限の場合もあり、これに対応するcosAの値は、第1象限なら正、第2象限なら負の値になる。(どちらも可能) ゆえに、cosA=±…(答) 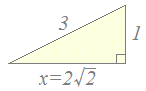 注意
注意右図のように直角三角形を描いて、三平方の定理を使って横の長さxを求めても答は得られるが、この解き方は「三平方の定理」の練習にはなるが三角比の相互関係の練習にはならない。 この方法ばかり練習していると、例えば(sinA+cosA)2などの変形ができないおそれがあります。 |
例2
cosA = (0°≦A≦180°)のときtanAの値を求めてください。
(答案) sin2A+cos2A=1にcosA = を代入すると
sin2A+cos2A=1にcosA = を代入するとsin2A+( )2=1 sin2A=1−= sinA=± 右図のようにcosA = のとき、Aは第1象限の角で、これに対応するsinAの値は正の数になる。 ゆえに、sinA= このとき、tanA= = = 2…(答)
(別解)
この答案では公式(1)を使ってcosA → sinA 公式(2)を使ってsinA , cosA → tanA のように2段階で求めたが、公式(3)を使って、cosA → tanAのように直接求めることもできる。 例3
tanA = − (0°≦A≦180°)のときcosAの値を求めてください。
■注意■
(答案)tanA = だからといって cosA = − 2 , sinA = などと考えていれば、大きな間違いです。 比率が− になるものには、 − , − , − など多くの分母・分子の 組合せがあります。 実際には、これらのうちでsin2A+cos2A=1を満たすものだけが答になりますが、その値は公式(3)で求まります。 公式(1)の両辺をcos2Aで割って、公式(3)を作る。 tan2A+1 = …(3) (3)にtanA = − を代入すると (− )2+1= = cosA=± 右図のようにtanA = − のとき、Aは第2象限の角で、これに対応するcosAの値は負の数になる。 ゆえに、cosA= − …(答) 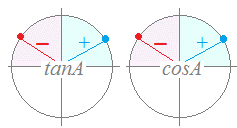
|
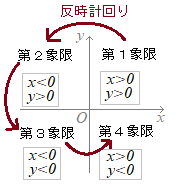 =>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.
=>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.