|
このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒ ２つの２次関数のグラフは，x2の係数aが一致すれば同じ形で，平行移動によって重なります．  【例1】
【例2】
|
  |
|
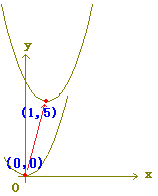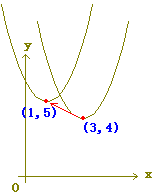このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒ ２つの２次関数のグラフは，x2の係数aが一致すれば同じ形で，平行移動によって重なります． 【例1】
【例2】
|
|
|
(4)
(A) ｙ＝－２ｘ2＋４ｘ＋５ (B) ｙ＝－２ｘ2－８ｘ＋１ 
ｙ軸の正の方向に (A) y=−2(x2−2x)+5=−2{(x−1)2−1}+5=−2(x−1)2+7の頂点は(1, 7) (B) y=−2(x2+4x)+1=−2{(x+2)2−4}+1=−2(x+2)2+9の頂点は(−2, 9) （x2の係数が等しいから，これらは同じ形） (A)をx軸の正の方向に−3，y軸の正の方向に2だけ平行移動すると(B)に重なる →閉じる← |
| (5)
(A) ｙ＝－５－ｘ2＋２ｘ (B) ｙ＝６ｘ－６－ｘ2
ｙ軸の正の方向に (A) y=−(x2−2x)−5=−{(x−1)2−1}−5=−(x−1)2−4の頂点は(1, −4) (B) y=−(x2−6x)−6=−{(x−3)2−9}−6=−(x−3)2+3の頂点は(3, 3) （x2の係数が等しいから，これらは同じ形） (A)をx軸の正の方向に2，y軸の正の方向に7だけ平行移動すると(B)に重なる →閉じる← |
|
■［個別の頁からの質問に対する回答］[２次関数の平行移動について／16.11.9］
今日の基礎力判定試験の範囲ってわかりますか？
＝＞［作者］：連絡ありがとう．?? 冗談を言っているのですか？どこかの予備校か学習塾の試験範囲のことなら，それをやっているところに尋ねないと･･･通りがかりのおじさんに尋ねてどうする． |
| ■このサイト内のGoogle検索■ |