2次不等式

→ 携帯版は別頁

== ２次不等式 ==

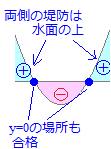
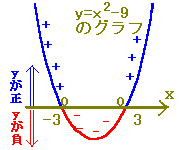
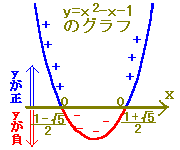
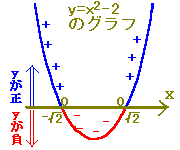
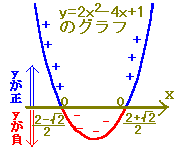
■■２次関数のグラフがx軸と２点で交わる場合■■
○　初めに2次関数のグラフが谷形になるものについて考えます。

y=ax2+bx+cにおいて２次の係数aが正であるとき，グラフは谷形になります。
⇒　y=ax2+bx+c（ただし，a>0）は谷形

○　　２次不等式
ax2+bx+c<0　（ただし，a>0）
は，yの値がy=ax2+bx+cの値に等しいグラフ，すなわち
y=ax2+bx+c　（a>0）
のグラフを利用して解くことができます．

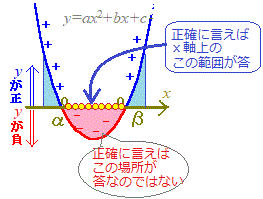
y=ax2+bx+c（a>0）のグラフでは
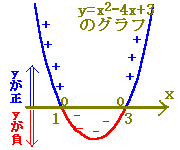
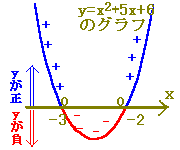
ax2+bx+cの値はy座標に等しいので，
ax2+bx+c<0
となるようなxの値の範囲はy<0となるようなxの値の範囲となります．（図の赤で示した部分）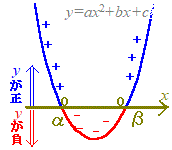

y=ax2+bx+cとx軸がx=α, βで交わるとき
y<0（すなわちyが負）となるのは
α<x<β
のときです．

右上に続く↑

→続き

※２次不等式の解き方を身に付けるためには，まず第１に，思い込みを捨てることが重要です．

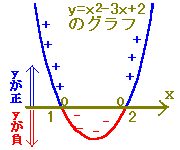
○すなわち，これまでに習った１次不等式の解き方では
$2x\lt 3\hspace{5}\rightarrow\hspace{5}x\lt\frac{3}{2}$
$4x\gt 5\hspace{5}\rightarrow\hspace{5}x\gt\frac{5}{4}$
のように,問題文の不等号の向きと解の不等号の向きが対応しています．xの係数が負の場合は，逆向きになりますが，それでも対応しています．
$-2x\lt 3\hspace{5}\rightarrow\hspace{5}x\gt-\frac{3}{2}$
$-4x\gt 5\hspace{5}\rightarrow\hspace{5}x\lt-\frac{5}{4}$

○これに対して，
x2−3x+2<0
のような２次不等式では，問題文の不等号が<であるからといって，解の不等号の向きが
x<1，x<2
となるのではなく，２次関数y=ax2+bx+cのグラフからyの符号が負になるようなxの範囲を探すことになります．
x2−3x+2>0
ではyの符号が正になるようなxの範囲を探すことになります．

※ここが核心※
不等式ax2+bx+c<0で求めているのはyの値の範囲ではなく，xの値の範囲です。（この式の変数はxだけ）

ここで２次関数y=ax2+bx+cを考えると、右辺は上の不等式の左辺の値となっています．
したがって、２次関数y=ax2+bx+cのyの値は上の不等式の左辺の値になります。

そこで、２次関数のグラフを利用して，「yの値（符号）が負になる」ような「xの値の範囲」を求めるということです。

　同様にして
ax2+bx+c>0 (a>0)
ax2+bx+c≦0 (a>0)
ax2+bx+c≧0 (a>0)
も解けます．

右上に続く↑

→続き

《要約》
ax2+bx+c=0の解がx=α, β (α<β)のとき

問題がax2+bx+c<0 (a>0)なら，

答はα<x<β
マイナスは「間」

問題がax2+bx+c>0 (a>0)なら，

答はx<α, β<x
プラスは「両側」

問題がax2+bx+c≦0 (a>0)なら，

答はα≦x≦β
マイナスは「間」
等号付き

問題がax2+bx+c≧0 (a>0)なら，

答はx≦α, β≦x
プラスは「両側」
等号付き

［例１］

２次不等式x2−x−12<0を解け。

（答案）

２次方程式x2−x−12=0を解くと (x+3)(x−4)=0より x=−3, 4	「２次不等式の問題なのに」問われていない「２次方程式」について演説を始めることが重要
２次関数y=x2−x−12のグラフは	「２次不等式の問題なのに」問われていない「２次関数」を描くことが重要グラフを描くためには、上で求めたｘ軸との交点の座標が必要になる･･･この問題を解くためには、頂点の座標などの正確な情報は不要。
グラフから、y<0すなわち２次不等式x2−x−12<0を満たすxの値の範囲は−3<x<4…（答）	ここでようやく「２次不等式」の話に戻る。マイナスになるのは「間（サンドイッチ）」が答

［例２］

２次不等式x2−x−12≧0を解け。

（答案）

２次方程式x2−x−12=0を解くと
x=−3, 4
２次関数y=x2−x−12のグラフは

グラフから、y≧0すなわち
２次不等式x2−x−12≧0を満たすxの値の範囲は
x≦−3 , 4≦x…（答）

　論理的に同じ内容を表していれば、次にように書いてもよい。
x≦−3 , x≧4
　筆者は、小さいものから大きいものへ左から順に並べていく書き方が「分かりやすく」「間違いにくい」と考える。

　例１と同様に、「不等式の問題を解くためには２次関数のグラフが必要、２次関数のグラフを描くためには２次方程式の解が必要」と考える。
　したがって、問われていなくても「２次方程式」→「２次関数」→「２次不等式」の順に述べることが重要。

プラスになるのは「両側」が答

※　問題に等号が付いているから、答にも等号を付ける。

よくある＃とんでもない答案＃
この問題の答を4≦x≦−3と書いてはいけない。
（4が−3よりも小さいということはない。そもそも、4≦xとx≦−3の両方を満たすようなxはなく、この問題の答となるxは２つの部分に分かれている。）
　一般に、「両側」形の範囲は、α≦x≦βの形にはまとめられない。

【問題】グラフを参考にして，２次不等式の解を選びなさい．（右から正しい選択肢をクリック） (1)	2次不等式 x2−4x+3<0 の解は 1<x, 3<x x<1, x<3 1<x<3 x<1, 3<x
(2)	2次不等式 x2+5x+6>0の解は −3<x, −2<x x<−3, x<−2 −3<x<−2 x<−3, −2<x
(3)	2次不等式 x2−4≧0の解は x≧±2 x≦±2 −2≦x≦2 x≦−2, 2≦x
(4)	2次不等式 x2−3x+2≦0の解は