|
پy‰ًگàپz •ھگ”‚â–³—گ”‚ھŒWگ”‚ة‚ب‚ء‚ؤ‚¢‚é‚ئ‚«‚إ‚àپCx‚جŒWگ”‚ھکa‚ة‚ب‚èپC’èگ”چ€‚ھگد‚ة‚ب‚é‚و‚¤‚ب‚Qگ”‚ً’T‚¹‚خ“¯‚¶‚و‚¤‚ة‚إ‚«‚ـ‚·پD —ل گد‚ھ کa‚ھ2‚ئ‚ب‚é‚Qگ”‚ح گد‚ھ |
|
پy‰ًگàپz پ¦ [1]پ`[IV]‚جŒِژ®‚ح’†ٹwچZ‚ج•œڈK‚ئ‚ب‚ء‚ؤ‚¢‚é‚ھپCچ‚چZ‚إ‚حپu’u‚«ٹ·‚¦پv‚ة‚و‚éˆِگ”•ھ‰ً‚ب‚ا‚â‚âچ‚“x‚ب‚à‚ج‚àٹـ‚ـ‚ê‚ؤ‚¢‚éپD ‹¤’تˆِگ”‚إ‚‚‚é
[I]پ@پ@ma+mb=m(a+b)
[I]‚ج—ل
(1)(2)
5x2y+20xy2=5(x2y+4xy2)=5xy(x+4y)
’چˆس
a+b ‚ج‚و‚¤‚بپuژ®‚ھ‹¤’تˆِگ”پv‚ئ‚ب‚邱‚ئ‚à‚ ‚éپD
پ@“r’†Œo‰ك‚ئ‚µ‚ؤ(1)‚ج‚و‚¤‚بژ®‚ًڈ‘‚‚ج‚حژ©—R‚إ‚ ‚éپi‰ً“ڑژز‚ھژv‚¢‚آ‚¢‚½ڈ‡ڈک‚ة‚و‚ء‚ؤ‚ح xy(5x+20y) ‚ب‚ا‘¼‚جŒ`‚ئ‚ب‚éڈêچ‡‚à‚ ‚蓾‚éپj‚ھپCچإڈIŒ`‚ح(2)‚جŒ`‚ة‚µ‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پD پ@‚آ‚ـ‚èپC‹¤’تˆِگ”‚ح‘S•”‚‚‚èڈo‚³‚ب‚¯‚ê‚خ‚ب‚炸پCچإڈIŒ`‚ة‚ـ‚¾‹¤’تˆِگ”‚ھژc‚ء‚ؤ‚¢‚é‚و‚¤‚بŒ`‚إ‚حگ³‰ً‚ئ‚ب‚ç‚ب‚¢پD
(a+b)x2−(a+b)x=(a+b)(x2−x)=(a+b)x(x−1)
b−a=−(a−b) ‚¾‚©‚çپCژں‚جژ®‚ح‹¤’تˆِگ”‚إ‚‚‚ê‚éپD
(a−b)x+(b−a)y=(a−b)x−(a−b)y=(a−b)(x−y)
ˆê”ت‚ةپCˆّ‚«ژZ‚جڈ‡ڈک‚ھ‹t‚ة‚ب‚ء‚ؤ‚¢‚é‚à‚ج‚حپu“¯‚¶ˆِگ”‚إ•„چ†‚¾‚¯‚ھ‹tپv‚ة‚ب‚éپDپ@y−x=−(x−y) ‚ب‚ا
پ¦‹¤’تˆِگ”‚إ‚‚‚é•دŒ`‚حپuŒِژ®‚ً—p‚¢‚éˆِگ”•ھ‰ً‚و‚è‚àگو‚ةچs‚¤پv•û‚ھ‚و‚¢پD —ل ‚»‚ج‚ـ‚ـ‚جŒ`‚إ‚حپ›2−پ 2‚جŒ`‚ةŒ©‚¦‚ب‚¢‚ھپC‹¤’تˆِگ”‚إ‚‚‚é‚ئ•ھ‚©‚é‚à‚ج
2x3−50x=2x(x2−25)=2x(x+5)(x−5)
|
| پy–â‘è1پzپ@ژں‚جژ®‚ًˆِگ”•ھ‰ً‚¹‚وپDپ@پiگ³‚µ‚¢‚à‚ج‚ًƒNƒٹƒbƒN‚¹‚وپDپj |
|
پy‰ًگàپz
[II]پ@پ@a2+2ab+b2=(a+b)2
[II]‚ج—ل
[III]پ@پ@a2−2ab+b2=(a−b)2 [IV]پ@پ@a2−b2=(a+b)(a−b)
9x2+6x+1=(3x)2+2·(3x)·1+12=(3x+1)2
پ،پ@—¼’[‚جژ® 3x , 1 ‚ًگو‚ةŒ©‚邱‚ئپDچإŒم‚ة’†‰›‚جچ€‚ھ‚»‚ê‚ç‚جگد‚ج 2 ”{‚ة‚ب‚ء‚ؤ‚¢‚ê‚خپiپ@پj‚ج‚Qڈو‚ئ‚µ‚ؤ‚و‚¢پD
پ،پ@‘O‚©‚çڈ‡‚ةŒ©‚ؤ‚¢‚‚ئژ¸”s‚·‚邱‚ئ‚ھ‘½‚¢پD [III]‚ج—ل
4x2−12xy+9y2=(2x)2−2·(2x)·(3y)+(3y)2=(2x−3y)2
پ،پ@ژں‚ج‚و‚¤‚بژ®‚حپC’†‰›‚جچ€‚ھ—¼’[‚ئ‚µ‚ؤچl‚¦‚é‚Pژںژ®‚جگد‚ج 2 ”{‚ة‚ب‚ء‚ؤ‚¢‚ب‚¢‚ج‚إپiپ@پj‚ج‚Qڈو‚ئ‚ح‚ب‚ç‚ب‚¢‚ج‚إ’چˆس‚·‚邱‚ئپD
[IV]‚ج—ل
4x2−9y2=(2x)2−(3y)2=(2x+3y)(2x−3y)
3x2−12=3(x2−4)=3(x+2)(x−2)
پ،Œِژ®‚ًچl‚¦‚é‘O‚ة‹¤’تˆِگ”‚إ‚‚‚ء‚ؤ‚¨‚پD
|
|
پy–â‘è2پzپ@ژں‚جژ®‚ًˆِگ”•ھ‰ً‚¹‚وپDپ@پiگ³‚µ‚¢‚à‚ج‚ً‘I‚×پDپj
(4)پ@5x3−45x
پثپ@ 3x(x+5)(x−5) پC 3x(x+9)(x−9) 5x(x+2)(x−2) پC 5x(x+3)(x−3) 5x(x+9)(x−9) پC ˆِگ”•ھ‰ً‚إ‚«‚ب‚¢ |
|
پy‰ًگàپz
[V]پ@پ@x2+(a+b)x+ab=(x+a)(x+b)
[V]‚ج—ل
x2+5x+6=x2+(2+3)x+2·3=(x+2)(x+3)
پ،پ@‚±‚ج‚و‚¤‚ب–â‘è‚إ‚حپC
پuچإڈ‰‚ةپv‚Qگ”‚جگد‚ھ 6 ‚ة‚ب‚é‘g‚ًچl‚¦‚邱‚ئپD پ@پ@1‚ئ6‚ج‘gپC2‚ئ3‚ج‘gپ@‚ھچl‚¦‚ç‚ê‚éپD پuژں‚ةپv‚»‚ê‚ç‚ج‚¤‚؟‚إ‚Qگ”‚جکa‚ھ 5 ‚ة‚ب‚é‘g‚ًچج—p‚·‚éپD پ@پ@1‚ئ6‚ج‘g پ¨ 1+6=7 پ~پ@پC2‚ئ3‚ج‘g پ¨ 2+3=5پ@پ› ‚±‚¤‚µ‚ؤپC(x+2)(x+3) ‚ً“ڑ‚¦‚ة‚·‚éپD پ¦پuچإڈ‰‚ةپv‚Qگ”‚جکa‚ھ5‚ة‚ب‚é‘g‚ًچl‚¦‚é‚ئپC‚¢‚‚ç‚إ‚à‚ ‚é‚©‚çچi‚è‚«‚ê‚ب‚¢پD
x2−7x+12=x2+(−4−3)x+(−3)·(−4)=(x−3)(x−4)
پ،پ@گد‚ھگ³‚جگ”12‚إپCکa‚ھ•‰‚جگ”−7‚ئ‚ب‚é‚Qگ”‚حپu•‰‚جگ”پv‚ئپu•‰‚جگ”پv‚ج‘g‚إ’T‚·پD
x2+2x−15=x2+(−3+5)x+(−3)·(5)=(x−3)(x+5)
پ،پ@گد‚ھ•‰‚جگ”−15‚ئ‚ب‚é‚Qگ”‚حپu•‰‚جگ”پv‚ئپuگ³‚جگ”پv‚ج‘g‚إ’T‚·پD
‚»‚ج‚¤‚؟‚إپCکa‚ھ2‚ئ‚ب‚é‚ج‚حپuگ³‚جگ”پv‚ھ‹‚¢•û‚ئ‚ب‚é |
|
پy–â‘è3پzپ@ژں‚جژ®‚ًˆِگ”•ھ‰ً‚¹‚وپDپ@پiگ³‚µ‚¢‚à‚ج‚ً‘I‚×پDپj
(3)پ@x2−10xy+24y2
پث (x−2)(x−8) پC (x−2y)(x−8y) پC (x−4)(x−6) (x−4y)(x−6y)پC (x−3)(x−8)پC(x−3y)(x−8y) |
|
پy‰ًگàپz •ھگ”‚â–³—گ”‚ھŒWگ”‚ة‚ب‚ء‚ؤ‚¢‚é‚ئ‚«‚إ‚àپCx‚جŒWگ”‚ھکa‚ة‚ب‚èپC’èگ”چ€‚ھگد‚ة‚ب‚é‚و‚¤‚ب‚Qگ”‚ً’T‚¹‚خ“¯‚¶‚و‚¤‚ة‚إ‚«‚ـ‚·پD —ل گد‚ھ کa‚ھ2‚ئ‚ب‚é‚Qگ”‚ح گد‚ھ |
|
پy–â‘è4پzپ@ژں‚جژ®‚ًˆِگ”•ھ‰ً‚¹‚وپDپ@پiگ³‚µ‚¢‚à‚ج‚ً‘I‚×پDپj
گد‚ھ
گد‚ھ
گد‚ھ
گد‚ھ
گد‚ھ−4‚إکa‚ھ
گد‚ھ9‚إکa‚ھ
|
|
پy‰ًگàپz
[VI]پ@پ@acx2+(ad+bc)x+bd=(ax+b)(cx+d)
[VI]‚ج—ل
پ،‚±‚جˆِگ”•ھ‰ً‚حپu‚½‚·‚«ٹ|‚¯ˆِگ”پv‚ئŒؤ‚خ‚ê‚é‚ھپCŒِژ®‚ًˆأ‹L‚µ‚ؤ‚à–â‘è‚ح‰ً‚¯‚ب‚¢پDژں‚ج—ل‚ج‚و‚¤‚ةپC‚Q‚آ‚¸‚آ‘g‚فچ‡‚ي‚¹‚ؤپu’†‰›‚جچ€پv‚ھˆê’v‚·‚é‚ـ‚إپu‚¢‚ë‚¢‚ëژژ‚µ‚ؤ‚ف‚éپv‚µ‚©‚ب‚¢پD
2x2+5x+3
x2 ‚جŒWگ”‚ئ‚µ‚ؤپCٹ|‚¯‚ؤ 2 ‚ة‚ب‚é‘g‚ح 1 ‚ئ 2 ‚¾‚©‚ç
(1x+…)(2x+…) ‚جŒ`‚ة‚ب‚éپD
’èگ”چ€‚ج•”•ھ‚حپCٹ|‚¯‚ؤ 3 ‚ة‚ب‚é‘g‚ح 1 ‚ئ 3 ‚¾‚©‚ç
(…+1)(…+3) ‚جŒ`‚ة‚ب‚éپD
‚»‚ê‚ç‚ج‘gچ‡‚¹‚حپC
پ@پ@(1x+3)(2x+1) …پiƒAپj ‚ئ پ@پ@(1x+1)(2x+3) …پiƒCپj
پiƒAپj‚حپC
پ@پ@···x2+(1·1+3·2)x+···=···x2+7x+··· ‚ة‚ب‚èپCچ‡‚ي‚ب‚¢ پiƒCپj‚حپC پ@پ@···x2+(1·3+1·2)x+···=···x2+5x+··· ‚ة‚ب‚èپCچ‡‚¤
پiƒCپj‚و‚èپC(x+1)(2x+3) …پi“ڑپj
پ،ڈم‚جپiƒAپjپiƒCپj‚ة‚¨‚¢‚ؤ x2 ‚جŒWگ”‚ئ’èگ”چ€‚حپCپuڈ‰‚ك‚©‚çچ‡‚¤‘gچ‡‚¹‚¾‚¯پv‚ًژg‚ء‚ؤ‚¢‚é‚©‚çپCڈ‘‚©‚ب‚‚ؤ‚àچ‡‚¤پD‚»‚±‚إپu‚Pژں‚جŒWگ”پv‚¾‚¯‚ةڈW’†‚µ‚ؤ‚±‚ê‚ًچ‡‚ي‚¹‚é‚و‚¤‚ة‚·‚éپDپ،‚±‚ê‚ç‚ج‚©‚¯ژZ‚ًڈcڈ‘‚«‚إڈ‘‚‚ئژں‚ج‚و‚¤‚ة‚ب‚éپD‚½‚¾‚µپC‚QژںپC’èگ”چ€پC‚Pژں‚جڈ‡‚ةڈ‘‚پD 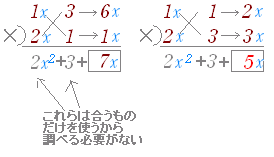 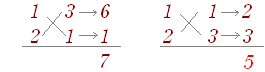 پ،‚±‚ê‚ç‚جŒvژZ‚ح‚·‚ׂؤپu‚Pژں‚جŒWگ”پv‚ھچ‡‚¤‚©چ‡‚ي‚ب‚¢‚©‚ً’²‚ׂ邽‚ك‚ج‚à‚ج‚إ‚ ‚éپD |
|
پy–â‘è5پzپ@ژں‚جژ®‚ًˆِگ”•ھ‰ً‚¹‚وپDپ@پiگ³‚µ‚¢‚à‚ج‚ً‘I‚×پDپj پ¦پ@“r’†ŒvژZ‚حٹeژ©‚إڈمگ}‚ج‚و‚¤‚ةچs‚¤‚±‚ئپD |
|
پ،پmŒآ•ت‚ج•إ‚©‚ç‚جژ؟–â‚ة‘خ‚·‚é‰ٌ“ڑپn[‚Qژںژ®‚جˆِگ”•ھ‰ً‚ة‚آ‚¢‚ؤپ^18.6.29پn
•ھ‚©‚è‚â‚·‚‚ؤ‚¢‚¢‚ئژv‚¢‚ـ‚·
پ،پmŒآ•ت‚ج•إ‚©‚ç‚جژ؟–â‚ة‘خ‚·‚é‰ٌ“ڑپn[‚Qژںژ®‚جˆِگ”•ھ‰ً‚ة‚آ‚¢‚ؤپ^17.12.09پn
پپپ„پmچىژزپnپFکA—چ‚ ‚è‚ھ‚ئ‚¤پD –â‘èگ”‚ً‘‚₵‚ؤ—~‚µ‚¢‚إ‚·پI
پ،پmŒآ•ت‚ج•إ‚©‚ç‚جژ؟–â‚ة‘خ‚·‚é‰ٌ“ڑپn[‚Qژںژ®‚جˆِگ”•ھ‰ً‚ة‚آ‚¢‚ؤپ^17.8.9پn
پپپ„پmچىژزپnپFکA—چ‚ ‚è‚ھ‚ئ‚¤پD‚P‚آ‚جƒyپ[ƒW‚ة–â‘è‚ً‹l‚كچ‚ٌ‚إ‚ ‚é‚و‚è‚àپC•K—v‚ة‰‚¶‚ؤ—lپX‚ب–â‘è‚ھ‚إ‚«‚é‚و‚¤‚ةپC‚¢‚‚آ‚©‚جƒyپ[ƒW‚ة•ھ‚¯‚ؤ‚ ‚è‚ـ‚·پDگو“ھ‚جƒTƒuƒپƒjƒ…پ[‚©‚çپC‘O‚ج‚ـ‚½‚حŒم‚ë‚جƒyپ[ƒW‚ً‘I‚ٌ‚إپC‘OŒم‚ج‹³چق‚ًŒ©‚ؤ‚‚¾‚³‚¢پD –â‘è5(1)‚ج‰ًگà‚إپuگو“ھ5‚ئ––”ِ-24پv‚ئ‚ ‚è‚ـ‚·‚ھپA––”ِ‚ج24‚ئ‚¢‚¤گ”ژڑ‚ح‚ا‚±‚©‚ç—ˆ‚ؤ‚¢‚é‚ج‚إ‚µ‚ه‚¤‚©پH
پپپ„پmچىژزپnپFکA—چ‚ ‚è‚ھ‚ئ‚¤پDٹm‚©‚ة•د‚إ‚·.
چ،‚ئ‚ب‚ء‚ؤ‚حپC‚ب‚؛ٹشˆل‚ء‚½‚ج‚©پCگ³ٹm‚ة‚ح•ھ‚©‚è‚ـ‚¹‚ٌ‚ھپCƒRƒپƒ“ƒg‚ًƒvƒچƒOƒ‰ƒ€‚إڈ‘‚¢‚ؤ‚¢‚½ژ‚ةپC‚¤‚ء‚©‚èڈ‘‚‚ئڈ¬ٹwگ¶‚إ‚àٹشˆل‚ي‚ب‚¢ژں‚ج‚و‚¤‚بٹشˆل‚¢‚ھ‹N‚±‚邱‚ئ‚ھ‚ ‚è‚ـ‚·پD
’ùگ³‚µ‚ـ‚µ‚½پD
1+1=11, 1+2=12, ..., 2+4=24 پiگ”ژڑ‚ج‰‰ژZ‚إ‚ح‚ب‚پC•¶ژڑ—ٌ‚ج’ا‰ء‚ئ‚ب‚ء‚ؤ‚¢‚éپj |
|
پm’چپn’¼‘O‚ةPC”إ‚©‚ç“ü‚ç‚ꂽڈêچ‡‚حپCژ©“®“]‘—‚إƒXƒ}ƒz”إ‚ة—ˆ‚ؤ‚¢‚ـ‚·‚ج‚إپCƒuƒ‰ƒEƒU‚جپm–ك‚éƒLپ[پn‚إ‚ح–ك‚ê‚ـ‚¹‚ٌپi“°پXڈ„‚è‚ة‚ب‚éپjپD‰؛‹L‚جƒٹƒ“ƒN‚ًژg‚ء‚ؤƒپƒjƒ…پ[‚ة–ك‚ء‚ؤ‚‚¾‚³‚¢پD
|