|
■要約■
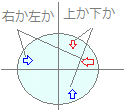
(1) 【これが全体の基本】
yと式が比較してあれば上下に分けて考える yが大きいのは上側 yが小さいのは下側 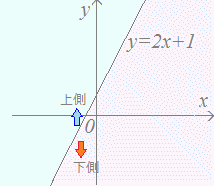 例 例・不等式y>2x+1の表す領域は、y=2x+1の直線の「上側」 ・不等式y<2x+1の表す領域は、y=2x+1の直線の「下側」  |
(2)
xと式が比較してあれば左右に分けて考える xが大きいのは右側 xが小さいのは左側 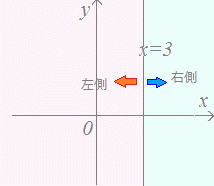 例 例・不等式x>3の表す領域は、 x=3の直線の「右側」 ・不等式x<3の表す領域は、 x=3の直線の「左側」
(3)
と式が比較してあれば原点からの距離が大きいか小さいかで考える x2+y2が大きいのは円の外側 x2+y2が小さいのは円の内側 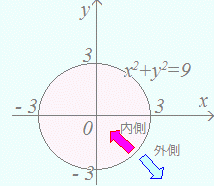 例 例・不等式x2+y2>9の表す領域は、 x2+y2=9の円の「外側」 ・不等式x2+y2<9の表す領域は、 x2+y2=9の円の「内側」 |
■解説■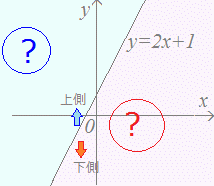 (はじめに) (はじめに)グランドをx ,y平面と考えたとき、方程式y=2x+1で表される直線はグランド全体から言えばわずかな場所しか表していない。中学校の幾何(図形)で習うように、正確に言えば「直線」には幅を考えないので、方程式で表されている直線の「面積」はグランド全体の面積と比べると無に等しいといえる。 では、圧倒的大多数の残りの部分はどんな式で表されるのか考えてみる。 一般に、幅を考えない直線や曲線に対して、広がりを持った場所のことを領域と言う。ここでは領域の表し方を考える。 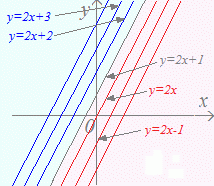 (1) y=2x+1のグラフをyの正の向きに1だけ平行移動したものがy=2x+2、2だけ平行移動したものがy=2x+3なので、
(1) y=2x+1のグラフをyの正の向きに1だけ平行移動したものがy=2x+2、2だけ平行移動したものがy=2x+3なので、y=2x+a (a>1)⇔ y=2x+a>2x+1の形で表される直線上にある点はy=2x+1のグラフよりも上にあることになる。
不等式y>2x+1を満たす点はy=2x+1のグラフよりも上にある。
同様にして、
不等式y≧2x+1を満たす点はy=2x+1のグラフよりも上で境界線を含む。
不等式y<2x+1を満たす点はy=2x+1のグラフよりも下にある。
不等式y≦2x+1を満たす点はy=2x+1のグラフよりも下で境界線を含む。 |
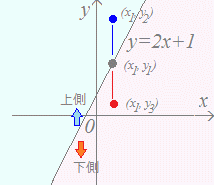 ■証明■ ■証明■y=2x+1のグラフ上にある点を(x1,y1)とおくと、 y1=2x1+1 …(A) が成り立つ。 y=2x+1のグラフよりも上にある点を(x1,y2)とおく。 このとき、x座標は等しく(x1)、y座標はy1<y2となる。 したがって、y2>y1=2x1+1 y2>2x1+1 …(B) が成り立つ。 このように、直線y=2x+1のグラフよりも上にある点の座標(x , y)は 同様にして、y=2x+1のグラフよりも下にある点を(x1,y3)とおくと、y3<y1=2x1+1 だから、直線y=2x+1のグラフよりも下にある点の座標(x , y)は |
 (2) x=3のグラフのようにy軸に平行な境界線で分けられている領域は、上か下かという分け方では表すことはできない。このような場合には、x座標が大きいか小さいか(右か左か)で分けることができる。
(2) x=3のグラフのようにy軸に平行な境界線で分けられている領域は、上か下かという分け方では表すことはできない。このような場合には、x座標が大きいか小さいか(右か左か)で分けることができる。
不等式x>3を満たす点はx=3のグラフよりも右にある。
不等式x≧3を満たす点はx=3のグラフよりも右で境界線を含む。
不等式x<3を満たす点はx=3のグラフよりも左にある。
不等式x≦3を満たす点はx=3のグラフよりも左で境界線を含む。 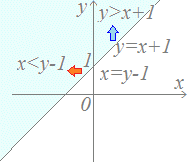 x座標の大小によって分ける方法は、(1)で述べたy座標の大小によって上下に分ける方法と矛盾しない。 x座標の大小によって分ける方法は、(1)で述べたy座標の大小によって上下に分ける方法と矛盾しない。右図のように不等式y>x+1で表される領域は、方程式y=x+1で表される直線の「上側」であるが、不等式x<y−1で表される領域は、方程式x=y−1で表される直線の「左側」であるといっても同じになる。 |
○ 一般に、上下に分けても左右に分けても示すことのできる領域は上下に分けて考えればよく、上下に分けて示せないときは左右に分ければよい。 例 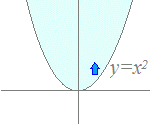 不等式y>x2の表す領域は方程式y=x2の表す曲線の上側 不等式y>x2の表す領域は方程式y=x2の表す曲線の上側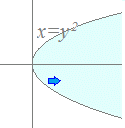 不等式x>y2の表す領域は方程式x=y2の表す曲線の右側 不等式x>y2の表す領域は方程式x=y2の表す曲線の右側 |
 (3) 円のように縦線で切っても横線で切っても境界線が2つできるような図形は、境界線よりも上(下)という示し方でも境界線よりも右(左)という示し方でも示すことができない。例えば、右の円は上の境界線:山形よりは下であるが下の境界線:谷形よりは上にあるから、円よりも上か下かということはできない。左右についても同様。
(3) 円のように縦線で切っても横線で切っても境界線が2つできるような図形は、境界線よりも上(下)という示し方でも境界線よりも右(左)という示し方でも示すことができない。例えば、右の円は上の境界線:山形よりは下であるが下の境界線:谷形よりは上にあるから、円よりも上か下かということはできない。左右についても同様。そこで、円の内部または外部の領域を不等式で表したいときは、yがある式よりも大きい(小さい)領域とかxがある式よりも大きい(小さい)領域という考え方をあきらめて別の方法を考える。 そもそも、円は中心からの距離が一定(半径rに等しい)であるような点なので、円周上の点の座標を(x , y)とおくと =r この方程式の左辺は中心(0 , 0)からの距離、右辺は半径の長さである。 例 原点を中心とする半径3の円の方程式は =3 通常は、両辺を2乗して根号を外した形で使う: x2+y2=9 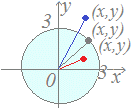 このように、円の中心(0 , 0)からの距離が半径よりも大きいか、小さいか、等しいかによって円の外側、内側、円周上に分けることができる。
このように、円の中心(0 , 0)からの距離が半径よりも大きいか、小さいか、等しいかによって円の外側、内側、円周上に分けることができる。 |
・中心からの距離が半径3よりも大きい場所(x , y)(円の外側)では
>3が成り立つ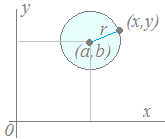 一般に、点(a , b)を中心とする半径rの円の外側、内側を不等式で表すには、中心(a , b)と点(x , y)との距離
一般に、点(a , b)を中心とする半径rの円の外側、内側を不等式で表すには、中心(a , b)と点(x , y)との距離が、半径rよりも大きいか小さいかで分けるとよいから、点(a , b)を中心とする半径rの円の内部、外部は次の不等式で表される。
円の外側(境界線を含まない)
|
例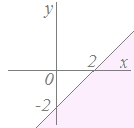 (1)-1 (1)-1不等式y≦x−2で表される領域は、直線y=x−2の下側(境界線を含む)  (1)-2 (1)-2不等式x−y−2>0で表される領域は 直線y=x−2の下側(境界線を含まない) 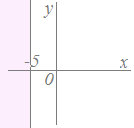 (2)-1 (2)-1不等式x<−5で表される領域は 直線x=−5の左側(境界線を含まない) 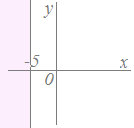 (2)-2 (2)-2不等式x+5≦0で表される領域は 直線x=−5の左側(境界線を含む) |
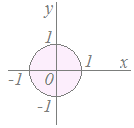 (3)-1 (3)-1不等式x2+y2<1で表される領域は 原点(0 , 0)を中心とする半径1の円の内側(境界線を含まない) 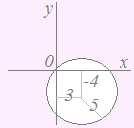 (3)-2 (3)-2不等式(x−3)2+(y+4)2>25で表される領域は 点(3 , −4)を中心とする半径5の円の外側(境界線を含まない) 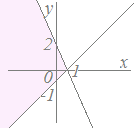 (4)-1 (4)-1連立不等式y<−2x+2 , y>x−1で表される領域は 直線y=−2x+2の下側かつ直線y=x−1の上側となる領域(境界線はすべて含まない) 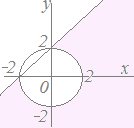 (4)-2 (4)-2連立不等式x2+y2>4 , y≦x+2で表される領域は 円x2+y2=4の外側かつ直線y=x+2の下側となる領域(ただし、直線y=x+2上の点は含まれない) ※ 連立不等式の表す領域は,与えられた不等式を全部満たす点だから,この問題で点(0 , 2) , (−2 , 0)は含まれない.…「含まれる」と「含まれない」とは対等に競合しているのではなく,「含まれない」が1つでもあれば「含まれない」の方が勝つ.(国連の安全保障理事会で拒否権を行使していると思えばよい) ■読み終わったら→ ここ ←をクリック■ |