■ 対数の計算
■解説
次の対数の定義を用いると(1)〜(5)が示せます。 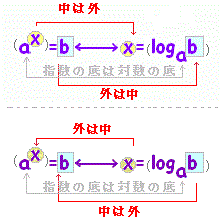 a>0 のとき,a0=1 だから,これを対数の形に直すと 0=loga1 となります。 (2)← a>0 のとき a1=a だから ,これを対数の形に直すと 1=logaa となります。 (2')← または,logaa-1 → - logaa → -1 |
(4)← |
■ 対数の計算
■解説
次の対数の定義を用いると(1)〜(5)が示せます。  a>0 のとき,a0=1 だから,これを対数の形に直すと 0=loga1 となります。 (2)← a>0 のとき a1=a だから ,これを対数の形に直すと 1=logaa となります。 (2')← または,logaa-1 → - logaa → -1 |
(4)← |
| [参考]
(3)(4) ○ 「和 → 積, 差 → 商」 ということですが 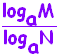 |
(5)
 また,次のように「対数にする」変形もよく使います。 2 = 2log22 = log24 |
|
【問題1】 次の式を簡単にしてください. (選択肢の中から正しいものをクリック)
(1)
(2)
|
(3)
(4)
|
|
(5)
(6)
|
(7)
(8)
|
|
(9)
(10)
|
(11)
(12)
|
|
【問題2】 次の式を簡単にしてください. (選択肢の中から正しいものをクリック) 分数
(1)
(2)
|
累乗根
(3)
(4)
|
|
係数が付いている場合
(5)
(6)
|
総合問題
(7)
(8)
|
|
(9)
|
(10)
|
|
■[個別の頁からの質問に対する回答][対数の計算について/17.5.9]
途中でlog/logやlog×logは当てはまらないと出て来ますがその場合の計算方法も載せて欲しい。
■[個別の頁からの質問に対する回答][対数の計算について/17.3.22]
=>[作者]:連絡ありがとう.そこに書いていますように「この式の変形は、後で出てくる底の変換が考えられる程度」です.すなわち, ただし,そこに書いていますように「底の変換の頁」を見てもらうと(2)は もう1点,どんな式でも変形できる公式があるに違いないと思い込んでいませんか?上記の(1)のような式は,もっと複雑にすることはできますが,これ以上簡単にする公式はありません.ないからないと書いているのです. 累乗根の問題で分母をアとウ、分子をイとエとするとわかりやすいと思います
■[個別の頁からの質問に対する回答][対数の計算について/17.4.3]
=>[作者]:連絡ありがとう.例えば「3分の2」の場合,3を先に読むじゃないかという話のようですが,センター試験問題などマークシート方式の問題で分母と分子を空欄にする場合は,分子から分母への順に名前を付けていくのが普通です.単なる習慣の違いで間違う生徒が出ないように,広く用いられる流儀に合わしています.なお,英語,コンピュータでは分子を先に読むようです:「3分の2」の場合,two thirds; 2 over 3; 2 by 3; fraction{2}{3} √の外し方教えてください
=>[作者]:連絡ありがとう.「√の外し方」と言えば中学校の話になりますが,対数計算とのかかわりで言えば,あなたが今やらなければならないのは対数関数の真数部分を累乗根から分数指数(有理指数)に直す変形です…(*1).(急がばまわれ:この頁とかこの頁を先に読まなければなりません) もう一つは,蚤の三段跳びの変形です…(*2). すなわち 次に「蚤の三段跳びの変形」(*2) |