|
■ 数学的帰納法(等式の証明)
[要点] ある等式(A)が成り立つことを数学的帰納法によって証明するには,次のようにすればよい. (I) n=1 のとき(A)が成り立つことを証明する. (II) n=k のとき(A)が成り立つことを仮定する. その仮定を使って n=k+1 のとき(A)が成り立つことを証明する. [例題1]
n が正の整数のとき,次の等式が成り立つことを証明せよ.
1+2+3+···+n=n(n+1) …(A)
[証明](I) n=1 のとき, 左辺=1 式(A)に 1+2+3+···+n と書いてあるからといって,左辺に +2+3 があると思ってはいけない.この左辺は初めの項を例として示すことにより,1 から n までの和であることを示している.だから,n=1 のときは,1つしかない.
右辺= 1(1+1)=1よって,n=1のとき(A)が成り立つ. (II) n=k のとき(A)が成立すると仮定すれば,
1+2+3+···+k= k(k+1) …(B)
(B)の両辺に k+1 を加えると
どこからそんな話が出てくるのか?それは,n=k+1 のときの左辺の形を予想すると,式(B)と +(k+1) の分だけ違うからである.
1+2+3+···+k+(k+1)= k(k+1)+(k+1)
= =
よって,n=k+1 のときも(A)が成立する.(I),(II) より,すべての正の整数 n について(A)が成り立つ. |
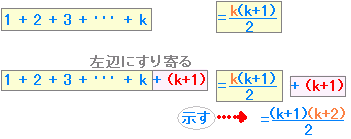
n=k のときと n=k+1 のときを比較すると
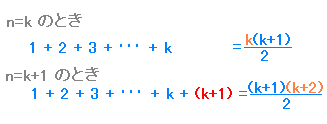  |
|
[例題2]
n が正の整数のとき,次の等式が成り立つことを証明せよ.
12+22+32+···+n2= n(n+1)(2n+1) …(A)
[証明](I) n=1 のとき, 左辺=12=1 右辺= 1(1+1)(2+1)=1 よって,n=1のとき(A)が成り立つ. (II) n=k のとき(A)が成立すると仮定すれば,
12+22+32+···+k2= k(k+1)(2k+1) …(B)
(B)の両辺に (k+1)2 を加えると
12+22+32+···+k2+(k+1)2
= k(k+1)(2k+1)+(k+1)2
= { k(k+1)(2k+1)+6(k+1)2 }
= (k+1){ k(2k+1)+6(k+1) }
= (k+1){ 2k2+7k+6 }
= (k+1)(k+2)(2k+3)
= (k+1)(k+2){2(k+1)+1}
よって,n=k+1 のときも(A)が成立する.(I),(II) より,すべての正の整数 n について(A)が成り立つ. |
(II) において次のように書いている答案は零点なので要注意
n=k のとき
12+22+32+···+k2=k(k+1)(2k+1)
n=k+1 のとき
12+22+32+···+k2+(k+1)2=(k+1)(k+2)(2k+3)
⇒ n=k のときも,n=k+1 のときも代入しているだけで何も証明されていない.n=k+1 のときも代入してしまうと,その式が n=k+1 のときに成立することを仮定していることになる.⇒ n=k のときは成立することを仮定しなければならないが,n=k+1 のときは成立することを証明しなければならない. |
|
[例題3]
n が正の整数のとき,次の等式が成り立つことを証明せよ.
13+23+33+···+n3= n2(n+1)2 …(A)
[証明](I) n=1 のとき, 左辺=13=1 右辺= 12(1+1)2=1 よって,n=1のとき(A)が成り立つ. (II) n=k のとき(A)が成立すると仮定すれば,
13+23+33+···+k3= k2(k+1)2 …(B)
(B)の両辺に (k+1)3 を加えると
13+23+33+···+k3+(k+1)3= k2(k+1)2+(k+1)3
=
=
=
=
よって,n=k+1 のときも(A)が成立する.(I),(II) より,すべての正の整数 n について(A)が成り立つ. |
(I) において次のように書いている答案は減点なので要注意
n=1 が成立するとき
1=1
⇒ (A)が成立するかどうか尋ねているのに,n=1 が成立する話をしても意味がない.
1=1
が成立することは小学生でも分かる.(A)が成立するかどうかについて述べられていない.
(II) において次のように書いている答案は減点なので要注意
n=k が成立するとき … … ⇒ (A)が成立するかどうか尋ねているのに,n=k が成立する話をしても意味がなく,(A)が成立するかどうかについて述べられていない. ⇒ 「 n=k のとき(A)が成立すると仮定すれば」と書かなければならない. |
|
[例題4]
n が正の整数のとき,次の等式が成り立つことを証明せよ.
1+2+22+23+···+2n-1=2n - 1 …(A)
[証明](I) n=1 のとき, 左辺=1 右辺=21 - 1=2 - 1=1 よって,n=1のとき(A)が成り立つ. (II) n=k のとき(A)が成立すると仮定すれば,
1+2+22+23+···+2k-1=2k - 1 …(B)
(B)の両辺に 2k を加えると
1+2+22+23+···+2k-1+2k=2k - 1+2k
=2 · 2k - 1=2k+1 - 1 (※)
よって,n=k+1 のときも(A)が成立する.(I),(II) より,すべての正の整数 n について(A)が成り立つ. |
公式 [指数法則]
a0=1
a1=a aman=am+n (A)の左辺は 10+21+22+23+···+2n-1 を表わしている. したがって,n=1 のとき,
左辺=20=1
n=2 のとき,
左辺=20+21=1+2
n=3 のとき,
左辺=20+21+22=1+2+4
になる.(※) 21 2k=2k+1 のように変形できる. |
|
[例題5]
n が正の整数のとき,次の等式が成り立つことを証明せよ.
[証明]1·2+2·3+3·4+···+n(n+1)= n(n+1)(n+2) …(A) (I) n=1 のとき, 左辺=1·2=2 右辺= 1(1+1)(1+2)=2 よって,n=1のとき(A)が成り立つ. (II) n=k のとき(A)が成立すると仮定すれば,
1·2+2·3+3·4+···+k(k+1)= k(k+1)(k+2) …(B)
(B)の両辺に (k+1)(k+2) を加えると
1·2+2·3+3·4+···+k(k+1)+(k+1)(k+2)
= k(k+1)(k+2)+(k+1)(k+2)
= {k(k+1)(k+2)+3(k+1)(k+2)}
= (k+1)(k+2)(k+3)
よって,n=k+1 のときも(A)が成立する.(I),(II) より,すべての正の整数 n について(A)が成り立つ. |
一般に次の関係が成り立つ
1+2+3+···+n
= n(n+1)
1·2+2·3+3·4+···+n(n+1)
= n(n+1)(n+2)
1·2·3+2·3·4+3·4·5+···+n(n+1)(n+2)
= n(n+1)(n+2)(n+3)
1·2·3·4+2·3·4·5+3·4·5·6+···+n(n+1)(n+2)(n+3)
= n(n+1)(n+2)(n+3)(n+4)
|