|
�@���̃y�[�W�ł́C�Q���`�R���̐����s��ɑ��āC�Ίp���C�W�����_���W���`�𗘗p���čs��̂�������߂���@�ׂ�D �y�W�����_���W���`�z �@���`�㐔�̋��ȏ��ł́C���҂ɂ���āC[A] �Ίp�s����܂߂ăW�����_���W���`�ƌĂԏꍇ�ƁC[B] �p��Ƃ��đΊp�s��ƃW�����_���W���`���Ă���ꍇ������̂ŁC���������Ăǂ���̗���ŏ�����Ă��邩����������K�v������D [A] �W�����_���W���`
[B]
�Ίp�s��
�W�����_���W���` 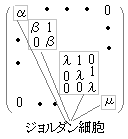 �E�}��\(\begin{pmatrix}\beta & 1\\0&\beta\end{pmatrix}\)��\(\begin{pmatrix}\gamma & 1&0\\0&\gamma&1\\0&0&\gamma\end{pmatrix}\)�̂悤�Ȍ`�̍s����W�����_���זE�ƌ����C�W�����_���זE��Ίp���ɉ����ĕ��ׂ��`�ɂȂ��Ă���s����W�����_���W���`�ƌ����D�������C�W�����_���זE�Ƃ���\(\begin{pmatrix}\alpha\end{pmatrix}\)��\(\begin{pmatrix}\mu\end{pmatrix}\)�̂悤��1�~1�`�̍s��܂Ŋ܂߂čl����̂�[A]�̗���ŁC�Ίp������������Ȃ�Ίp�s��͕ʂɍl����̂�[B]�̗���ƂȂ��Ă���D���t�̎g�������Ⴄ�����D
�E�}��\(\begin{pmatrix}\beta & 1\\0&\beta\end{pmatrix}\)��\(\begin{pmatrix}\gamma & 1&0\\0&\gamma&1\\0&0&\gamma\end{pmatrix}\)�̂悤�Ȍ`�̍s����W�����_���זE�ƌ����C�W�����_���זE��Ίp���ɉ����ĕ��ׂ��`�ɂȂ��Ă���s����W�����_���W���`�ƌ����D�������C�W�����_���זE�Ƃ���\(\begin{pmatrix}\alpha\end{pmatrix}\)��\(\begin{pmatrix}\mu\end{pmatrix}\)�̂悤��1�~1�`�̍s��܂Ŋ܂߂čl����̂�[A]�̗���ŁC�Ίp������������Ȃ�Ίp�s��͕ʂɍl����̂�[B]�̗���ƂȂ��Ă���D���t�̎g�������Ⴄ�����D
|
�@3�������s��̏ꍇ���ɂƂ��āC�ȉ��̂��̃y�[�W�̋��ނɏ�����Ă��邱�Ƃ̗v��������Ǝ��̒ʂ�D
�y�v��z
�@�͂��߂ɗ^����ꂽ�s�� (1)�@�ŗL�l �ƂȂ�ŗL�x�N�g�� �Ƃ����ƁC���̕ϊ��s��͐����ɂȂ�i�t�s�� �@�ŗL�l��Ίp�����ɂ����Ίp�s��� �Ƃ����� �������� �����藧��. �@���̂Ƃ��C
���̋��ނɎ�������̗�
�@�Ίp�s��͍s��̐ςƂ��Ă̗ݏ悪�e�ՂɌv�Z�ł���̂ŁC����𗘗p���čs��̗ݏ���v�Z���邱�Ƃ��ł���D�y��1.1�z �y��1.2.1�z �y��1.2.2�z �y��1.3.1�z �y��1.3.2�z |
|
(2)�@�ŗL���������d�������ꍇ�C �@�j�@���̍s�̂��Ίp�s��ł���Ƃ� �@�����̍s��́C�ϊ�����܂ł��Ȃ��Ίp�s��ɂȂ��Ă��邩��C����Ȃǂ̌v�Z�͗e�Ղɂł���D �A�j�@��L���@�j�ȊO�ŌŗL���������d���������Ƃ��C���̂悤�ɃW�����_���W���`�ƌĂ��`�ɂł��� �@A)�@�d���x1�̉�
a) �C�ӂ̃x�N�g��
�ƂȂ��x�N�g�� �Œ�܂�ϊ��s�� �Ə������Ƃ��ł���D
���̋��ނɎ�������̗�
b) ��2�������s��� �y��2.1�z(1) �y��2.2.1�z�y��2.2.2�z�y��2.2.3�z�y��2.2.4�z ��3�������s��� �y��2.1�z(2) �y��2.3.1�z �y��2.3.2�z �ƂȂ��x�N�g�� �Œ�܂�ϊ��s�� �Ə������Ƃ��ł���D
���̋��ނɎ�������̗�
�y��2.3.3�z �y��2.3.4�z �y��2.3.5�z |
�@B)�@�O�d��
�@�Ȃ�,2�������s��ŌŗL�l���d��
a) �C�ӂ̃x�N�g��
�ƂȂ�x�N�g�� �Œ�܂�ϊ��s�� �Ə������Ƃ��ł���D
���̋��ނɎ�������̗�
�y��2.4.3�z �y��2.4.4�z
b) �C�ӂ̃x�N�g��
�ƂȂ�x�N�g�� �Œ�܂�ϊ��s�� �Ə������Ƃ��ł���D
���̋��ނɎ�������̗�
�y��2.4.1�z �y��2.4.2�z �����藧�ĂC���ʏ�̔C�ӂ̃x�N�g���� �ƂȂ�D���������� �ƂȂ�C���̂悤�Ȃ��Ƃ��N����̂� �@���l�ɂ��āC3�������s��ŌŗL�l���O�d���ƂȂ�ꍇ�ɂ����āC1���Ɨ��ȂR�̃x�N�g�� �����藧�ĂC��ԓ��̔C�ӂ̃x�N�g���� �ƂȂ�D���������� �ƂȂ�C���̂悤�Ȃ��Ƃ��N����̂� �@����炪(2)�@)�ɏq�ׂ����̂ł���D |
|
1.1�@�Ίp���\�ȍs��̏ꍇ
�@�^����ꂽ�s��s��̗ݏ�����߂�v�Z�͈�ʂɂ͓���D�������C���̂悤�ȑΊp�s��ł͗e�Ղɂ�������߂邱�Ƃ��ł���D�����ŁC ���l�ɂ��āC��ʂɎ��̎������藧�D ���ӂɍ����� �@���̂悤�ɁC |
�y��1.1�z
(1)(1) (2) ���Ȃ킿 �����藧���� (2) �����藧�D���Ȃ킿 |
|
1.2 �Ίp���ł���ꍇ�̑Ίp�s��̋��ߕ�(���ۂ̌v�Z)
�@�Q���̐����s���ꎟ�ϊ� �ƂȂ邱�Ƃ������D �@���l�ɂ��āC�ŗL�l �ꎟ�ϊ� �ƂȂ邱�Ƃ������D (1)(2)���܂Ƃ߂�Ǝ��̂悤�ɏ�����D |
�@�ŗL�l�����قȂ�d�����������Ȃ��Ƃ��C���Ȃ킿 �@�����ŁC ���Ȃ킿 �̌`�őΊp���ł��邱�ƂɂȂ�C�Ίp�s��͗ݏ��e�ՂɌv�Z�ł���̂� �ɂ�� |
|
�y��1.2.1�z
�i�j(1) �@�ŗL������������ �@�ŗL�x�N�g�������߂� �A�j ���Ȃ킿 ��� �P�̌ŗL�x�N�g���Ƃ��āC �C�j ���Ȃ킿 ��� �P�̌ŗL�x�N�g���Ƃ��āC �A�j�C�j��� �܂Ƃ߂ď����� |
�y��1.2.2�z
�i�j(2) �@�ŗL������������ �@�ŗL�x�N�g�������߂� �A�j ���Ȃ킿 ���P�̌ŗL�x�N�g���Ƃ��āC ���l�ɂ��� �C�j �E�j �ȏ�̌��ʂ��܂Ƃ߂�� |
|
1.3�@�ŗL�l�������̏ꍇ
�@�����s��ɈقȂ�ŗL�l�݂̂������āC�ŗL�l�ɏd�����Ȃ��ꍇ�ɂ́C�Ίp���ł���D�@���̍s���W���̍s��ł���Ƃ��C�����̌ŗL�l�ł����Ă������̌ŗL�l�ł����Ă��d�����Ȃ���ΑΊp���ł���D �@���̍s���W���̍s��ł����āC�����̌ŗL�l���o�ꂷ��ꍇ�ł��s���n��̐����͎����ɂȂ�---�����̌ŗL�l�ƌ����Ă����f���̑��琬��C�����̘a��ςŕ\�����s���n��́C�����ŏ�����D
�y���1.3.1�z
�i�j�@���̍s�� �@�ŗL������������ �@�ŗL�x�N�g�������߂� �A�j ��� �C�j ��� |
�A�j�C�j��� �@�䂦�ɁC�s��
���̕\���g���Ă܂Ƃ߂��
1�jn=4k�̂Ƃ� 2�jn=4k+1�̂Ƃ� 3�jn=4k+2�̂Ƃ� 4�jn=4k+3�̂Ƃ�
���_�̉��Ɋp��������]����1���ϊ�
�ɓ��Ă͂߂�ƁC �ō��̌v�Z�ƈ�v���� |
|
�y���1.3.2�z
�i�j�@���̍s�� �@�ŗL������������ �@�ŗL�x�N�g�������߂� �A�j ��� �C�j ��� �A�j�C�j��� �@�䂦�ɁC�s�� |
�����ŕ��f���̋ɕ\�����l����� �����ŁC ������ ���� �ȉ� ���̂悤�ɁC���̍s��̐����������ł���C���̌ŗL�l��ŗL�x�N�g���������ł����Ă��C�i�\�z�ʂ�Ɂj����͎����ɂȂ邱�Ƃ�������D �i�ʉ��j ���_�̉��Ɋp��������]���āC���Ɍ��_����̋�����r�{���邱�Ƃ�\���P���ϊ��̍s��� �ł���C�^����ꂽ�s��� �Ə����邩�� ����]��\���s��ɂȂ���̂���ł͂Ȃ�����C�O�q�̂悤�ɋ����̌ŗL�l�C�ŗL�x�N�g���Ŏ������Ă݂�Ӌ`�͂���D |
|
2.1�@�Ίp���͂ł��Ȃ�������ɋ߂��`�ɂł���ꍇ
�@�s��̌ŗL�l���d���ɂȂ�ꍇ�Ȃǂɂ����āC�Ίp���ł��Ȃ��ꍇ�ł��C���̂悤�ɑΊp�����̂P��̐�����1�ɂ����`�𗘗p����Ɨݏ�̌v�Z���ł���D
�y��2.1�z
(1)(1) (2) |
���Ȃ킿 �����藧���� (2) �����藧�D���Ȃ킿 |
|
2.2 �W�����_���W���`�̋��ߕ�(���ۂ̌v�Z)
�y���2.2.1�z
�i�j(1)�@���̍s�� �@�ŗL�������������ČŗL�l�����߂� �@�ŗL�x�N�g�������߂� ���Ȃ킿 ���P�̌ŗL�x�N�g���Ƃ��āC
[�ȉ��̉������@] �ƂȂ�
�@�����Ȃ�C����Șb���Ȃ�������̂��^��Ɏv����������Ȃ��D
�@���́C���̒i�K�ł� |
���ӂ̐������r����� ������C �P�̌ŗL�x�N�g���Ƃ��āC ����ɂ�� ���Ȃ킿 �i�Q�l�j ���̌�C���̂悤�ɕό`����Ζ��̍s��`�̂��悪�v�Z�ł���D |
|
[�ȉ��̉������A] �P�̌ŗL�x�N�g���Ƃ��āC |
�i�Q�l�j ���̌�C���̂悤�ɕό`����Ζ��̍s��`�̂��悪�v�Z�ł���D ���̌��ʂ͇@�̌��ʂƈ�v���� |
|
[�ȉ��̉������B] ���`�㐔�̋��ȏ��C�Q�l���ɂ́C���̂悤�ɏ�����Ă��邱�Ƃ�����D �@�s�� �����̎��̈Ӗ��͎��̂悤�ɂȂ��Ă���
(1)�͌ŗL�l��
���ڍ������ �Ƃ���(1)������D �@����ɑ��āC(2)�͎��̂悤�ɕ����čl����� ��\���Ă��邱�Ƃ�������D ���x�N�g���ɕ������ ��(1)��\���Ă��� ��(2)��\���Ă���D (2)�� �Ə�����D�v�����(1)�����ŗL�x�N�g�������߂Ă���� ���� �ȏ�̂��Ƃ͍s��ƃx�N�g���ŏ�����Ă���̂ŁC�K������������Ղ��Ƃ͌����Ȃ����C�������@�ɂ����� �ƂȂ� |
�y�������B�̂܂Ƃ߁z
[�ȉ��̉������B]�ƂȂ�x�N�g�� �́C���̍s�� �����藧�D ���ۂɉ����Ă݂�ƥ�� �s�� �����ŁC���̕������������āC (1)��� ���������āC �����ŁC ����(2)�ɂ�� ���������āC �����ŁC |
|
[�������B�̂Q]����ʂ̉�� �@���`�㐔�̋��ȏ��C�Q�l���ɂ���ẮC���̂悤�ɉ�������ꍇ������D �@�͂��߂ɁC��x�N�g���łȂ��i���ŗL�x�N�g�� �@�O�̉����(1’)(2’)�̎��͓����ł��邪�C�u |
�Ƃ����� �@���̏ꍇ�C�C�ӂ̃x�N�g���͌ŗL�x�N�g�� �@�Ⴆ�C�C�ӂ̃x�N�g���� �ƂȂ��� ��������D �@���ߊ����܂ł́C�l������������C���ꂽ��P����Ƃŋ��߂���悤�ɂȂ�D |
|
�y���2.2.2�z
�i�j�@���̍s��̃W�����_���W���`�����߂āC �ŗL�l�����߂� ��� ����āC�P�̌ŗL�x�N�g����
(�������@)
���̃x�N�g�� �Ƃ����� �ƂȂ�C�Ίp���͂ł��Ȃ��Ă��C����ɏ������O�p�����ł���D �䂦�ɁC �Ⴆ��1�̉��Ƃ��� �Ƃ���ƁC ���Ȃ킿 �ƂȂ邩�� ���� |
�@�O�q�ɂ����āC(�������@)�Ŏ��������ẮC(**)�������̃x�N�g�����g���Ă��C�������ʂ�������D (�������A) �Ⴆ��1�̉��Ƃ��� �Ƃ���ƁC ���Ȃ킿 �ƂȂ邩�� ���� �ƂȂ��āC���ʂ͓������Ȃ�D �i�������B�j �s�� �����ŁC���̕������������āC (1)��� ���������āC �����ŁC ����(2)�ɂ�� �����ŁC �@�ȉ��́i�������@�j�i�������A�j�Ɠ��l�ɂȂ�D (�������B�̂Q) �Ⴆ�� �ƂȂ� ������C���Ɍv�Z����ƁC��L(�������@)(�������A)�̌��ʂƈ�v����D |
|
�y���2.2.3�z
(�������@1)�@���̍s��̃W�����_���W���`�����߂āC �@�ŗL������������ ��� ����āC�P�̌ŗL�x�N�g���� ������ �ƂȂ� ��� ���Ȃ킿 �ƂȂ邩�� |
�i�������A�j (**)�ɂ����� ���Ȃ킿 �ƂȂ邩�� �i�������B�j �s�� �����ŁC���̕������������āC (1)��� ���������āC �����ŁC ����(2)�ɂ�� �����ŁC �@�ȉ��́i�������@�j�Ɠ��l�ɂȂ�D �i�������B�̂Q�j �ŗL�x�N�g�� ���߂�� ���Ȃ킿 �ƂȂ邩�� |
|
�y���2.2.4�z
(�������@)�@���̍s��̃W�����_���W���`�����߂āC �@�ŗL������������ ��� ����āC�P�̌ŗL�x�N�g���� ������ �ƂȂ� ��� ���Ȃ킿 �ƂȂ邩�� |
�i�������A�j (**)�ɂ����� ���Ȃ킿 �ƂȂ邩�� �i�������B�̂Q�j �ŗL�x�N�g�� ���߂�� ���Ȃ킿 �ƂȂ邩�� |
|
2.3�@�R�������s��ŌŗL�l����d���ɂȂ�ꍇ
�R�������s����W�����_���W���`�ɂ���ƁC�s��̂��悪���̂悤�Ɍv�Z�ł���
�y���2.3.1�z
�i�������@�j�@���̍s��̃W�����_���W���`�����߂Ă��������D �ŗL������������ �ŗL�x�N�g�������߂� �A�j ��� �C�j ��� |
�����Q�̃x�N�g���ƂP���Ɨ��ȃx�N�g���������P���߂�K�v�����邩�� �ƂȂ�x�N�g�� �ȏ�ɂ�� �ƂȂ� �i�������B�̂Q�j ���߂�D ���Ƃ��C |
|
�y���2.3.2�z
�i�������@�j�@���̍s��̃W�����_���W���`�����߂Ă��������D �ŗL������������ �ŗL�x�N�g�������߂� �A�j ��� �C�j ��� |
�����Q�̃x�N�g���ƂP���Ɨ��ȃx�N�g���������P���߂�K�v�����邩�� �ƂȂ�x�N�g�� �ȏ�ɂ�� �ƂȂ� �i�������B�̂Q�j ���߂�D ���Ƃ��C |
|
�@2�������s��d�������Ƃ��C���̍s�̂��P�ʍs��̒萔�{�ł���ꍇ�������C�Ίp���ł��邱�Ƃ͂Ȃ��W�����_���W���` �ɂȂ�D �@����ɑ��āC3�������s�P�̉� �ƂȂ��x�N�g�� �Œ�܂�ϊ��s�� �Ə������Ƃ��ł���D
�y���2.3.3�z
�ŗL�������������@���̍s�Ίp���\���ǂ������ׂĂ��������D |
�ŗL�x�N�g�������߂� �A�j �C�j ��������x�N�g���͓Ɨ��ɂQ�ł��� �ȏ�ɂ�� �ϊ��s�� �Ίp�s�� ���Ȃ킿 |
|
�y���2.3.4�z
�i�����j�@���̍s�Ίp���\���ǂ������ׂĂ��������D �ŗL�l �ŗL�l �Ίp���\ |
�y���2.3.5�z
�i�����j�@���̍s�Ίp���\���ǂ������ׂĂ��������D �ŗL�l �ŗL�l �Ίp���\ |
|
2.4�@�R�������s��ŌŗL�l���O�d���ɂȂ�ꍇ
�R�������s����W�����_���W���`�ɂ���ƁC�s��̂��悪���̂悤�Ɍv�Z�ł���
�O�d���̏ꍇ�C���̌`���g���邱�Ƃ�����D ���̌`�ł͂��Ȃ蕡�G�ɂȂ�
�y���2.4.1�z
�i�������@�j�@���̍s��̃W�����_���W���`�����߂āC������v�Z���Ă��������D �ŗL������������ �ŗL�x�N�g�������߂� ��������x�N�g���͂P���Ɨ��ɂQ���� |
�����ȕϊ��s������ɂ́C�����P�P���Ɨ��ȃx�N�g�����K�v�����玟�̌`�ŃW�����_���W���`�����߂� ��� �ȏ�ɂ�� ������v�Z����ɂ́C���̌����𗘗p���� |
|
�i�������B�̂R�j 1���Ɨ��ȃx�N�g���̑����������s�� �����̌`�ŃW�����_���W���` �ƂȂ�悤�Ƀx�N�g�� ���ӂ��x�N�g���ɕ������ ���Ȃ킿 �����ŁC�C�ӂ́i�������C��ŋ��܂�x�N�g�� |
�@�Ⴆ�C (1’)�͎��̌`�ɏ����� �@���̂Ƃ��C �ɂ��āC �ϊ��s��͉������@�Ɠ����ł͂Ȃ����C����̌v�Z�l�ɍs���ƁC���ʂ͓����ɂȂ� |
|
�y���2.4.2�z
�i�����F�������B�j�@���̍s��̃W�����_���W���`�����߂��������D �ŗL�������͎O�d�� ����ɑΉ�����ŗL�x�N�g�������߂� ��� ��������x�N�g���͓Ɨ��ɂQ�I�ׂ� |
�����ƓƗ��ɂ���1�x�N�g�� �ƂȂ�x�N�g�� �ȏ�ɂ�� �����ȕϊ��s�� �W�����_���W���` �Ƃ��� �����藧�D |
|
�y���2.4.3�z
�i�������B�̂Q�j�@���̍s��̃W�����_���W���`�����߂āCn����v�Z���Ă����������������D �ŗL������������ ���̌`�ŃW�����_���W���`�����߂� �����ȕϊ��s��͂R�̂P���Ɨ��ȃx�N�g���𑩂ɂ������̂Ƃ��� ���ӂ��x�N�g���ɕ������ ���Ȃ킿 �@���̏��Ɍ��߂�F�C�ӂ́i�������C��ŋ��܂�x�N�g�� |
�@�Ⴆ�� �Ƃ����� �ƂȂ�D �ȏオ�W�����_���W���`�ł��� n��͎��̌������g���ċ��߂� |
|
�y���2.4.4�z
�i�������B�̂Q�j�@���̍s��̃W�����_���W���`�����߂āCn����v�Z���Ă����������������D �ŗL������������ �ϊ��s������߂�D �C�ӂ̃x�N�g�� �ƂȂ� �@�Ⴆ�C���̂悤�ɒ�܂�D ������ �Ƃ����� �ɂ�� ����� �ɂ�� �Ȃ� �����藧�D |
(#1)��
�ȏ�ɂ�����Ȃ킿 ��\���Ă���. (#2)�� ���Ȃ킿 ��\���Ă���. (#3)�� ���Ȃ킿 ��\���Ă���. (#1’)(#2’)(#3’)���ϊ��s��� �i�E�ӂ̃W�����_���W���`�ɂ����āC�P��ڂ� �ɑ��āC�ϊ��s�� �W�����_���W���` �Ƃ����� �����藧�D���Ȃ킿 ������ |