■連立不等式
問題１　　次の連立不等式を解け．　　[ 第1問 / 全8問中 ]
○==メニューに戻る
■解説
○　連立不等式とは

　連立不等式とは２つ以上の不等式を組み合わせたものをいい，それらの不等式をすべて満たす値の範囲を連立不等式の解という．

　連立方程式と名前は似ているが，解き方が全く異なる．

　すなわち，連立方程式では未知数が２つ以上あって，各式を足したり引いたりして未知数の個数を減らして解くことが多いが，以下の頁で扱う連立不等式は文字は１個で，各不等式を１つずつ解く．
連立方程式の例
2x+y=2
3x - y=8 		連立不等式の例
2x+1>3 …(1)
3x - 1≦8 …(2)
○　右の連立不等式 (1)(2)は次のように解く．
　(1)より　x>1
　(2)より　x≦3
これらを右図のように図示し，共通部分を考えて
1<x≦3…（答）
【 要約 】　連立不等式の解き方
  • 各不等式を１つずつ解く．
  • それらを数直線上に図示して共通部分を答にする．
参考
  • 1<x かつ x≦3 ようにサンドイッチ形になる範囲は，
    1<x≦3 とつなげて書く．
  • 1<x かつ 3≦x ように，大きい方と大きい方の組合わせでは，「共通部分」は狭い方になる．
参考
  • 等号なしの不等号は「白丸」「斜め線」で図示し，等号付不等号は「黒丸」「垂直線」で図示する．（図が複雑になると，この二重の安全装置のおかげで助かることが多い．）
  • 範囲を表わす「横線」は１つずつ高さを変えること．（下の「悪い書き方」では混乱してしまって分からなくなる．）
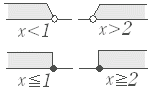
【 要約 】　次のような形の不等式は連立不等式に直して解ける．
- 1<2x+1<x+4
⇔
- 1<2x+1 …(1)
2x+1<x+4 …(2)
 例：（左の問題の答案）
- 1<2x+1 …(1)
2x+1<x+4 …(2)
(1)より - 1<x
(2)より x<3
以上から - 1<x<3 …（答）
○==メニューに戻る