等式 x+y=5 を x=5 - y に変形したり, S= を h= に変形することは, 次に習う方程式の解き方において基本となる技術です. |
 |
等式 x+y=5 を x=5 - y に変形したり, S= を h= に変形することは, 次に習う方程式の解き方において基本となる技術です. |
 |
|
【例題】 次の等式を[ ]内に示された文字について解きなさい. (1) x+y=5 [ y について] |
[考え方] x+y=5 において,y 以外のものを右辺に持っていく. x を移項する y=−x+5…(答)( y=5−x でもよい.) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
(2) 3xy=5 [ y について] |
[考え方] 3xy=5 において,y 以外のものを右辺に持っていく. 両辺を 3x で割る y=…(答) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
(3) 2(x+y)=m [ y について] |
[考え方] 「かっこ」をはずす. 2x+2y=m 2x を移項する 2y=m−2x 両辺を 2 で割る y=…(答) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
(4) m= [ y について] |
[考え方] 分母をはらう. 2m=x+y 左辺と右辺を入れ替えて,y を左辺に連れてくる. x+y=2m x を移項する y=2m−x…(答) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
### そもそも,何を求めているのか ### *** 答を見ても「なぜそれが答なのか分からない」という人へ *** 「y について解きなさい」という問題の答は,必ず「y=1とかy=2のような数字でなければならない」と思い込んでいると,この問題は答を聞いてもなぜそれが答なのか分からないことになります. ○上の例題(1)の問題は次の形をしています.
x+y=5をyについて解きなさい
これが成り立つような,x, yの値を調べてみると,次の表で上下に示したx, yの組はどれもx+y=5を満たしています.
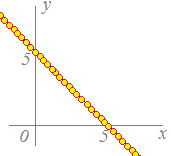
図で示すと,次の○印のようにx+y=5の直線上にある点の座標 (x, y)はすべて答になり,答は無限にあることになります. だから,1つの数字でy=?という形の答を期待することは無理なのです. では,「yについては何も決まらないのか?」というと,そうでもありません. 上の表1でも表2でもxが決まればyは決まります. x+y=5 を変形して y=5−x …(*) にしてみると,表1,表2の全部の値がこれを満たしていることが分かります. この(*)式のように,
yを他の文字や数字を使って,y=...の形で表すことを「yについて解く」というのです.
○もし問題が
xy=6をyについて解きなさい
という形をしていたら,今度は次の表3のようなx, yの組で成り立つことになります.
このような場合でも,xを決めたらyは決まります. を変形して ○要約すると なにかある等式が与えられたときに,その式を「yについて解く」とはy=...の形に変形することを言います. この変形だけでは,「それが何の役に立つのか」分かりにくいですが,この変形ができると他の式に代入して文字の個数を減らすなど応用が開けてくるのです. もちろん,「xについて解く」とはx=...の形に変形することを言い,「aについて解く」とはa=...の形に変形することを言います... |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題】
次の等式を[ ]内に示された文字について解きなさい.・・・半角小文字で入力しなさい.分数になるときは分母の符号は正にして表わしなさい. |
 |
x−y=3 の x を右辺に移項する. −y=−x+3 両辺に −1 を掛ける. y=x−3 →閉じる← |