|
�������̃y�[�W���̖ڎ����� ����i�N���b�N����C���̍��ڂփW�����v�ł��܂��j
(1)�@�W��A�̗v�f�̌���\���L��n(A)
(2)�@�W���̗v�f�̌��Ɋւ���藝
n(A∪B)=n(A)+n(B)−n(A∩B)
(����) ��W���̗v�f�̌�
n(A)=n(U)−n(A)
(����) 3�̏W���̗v�f�̌��@�@�h�E�����K���̖@���ŕό`�ł������ n(A∪B)=n(A∩B) n(A∩B)=n(A∪B)
n(A∪B∪C)=n(A)+n(B)+n(C)
���������̓W�J�E�����ɂ�������−n(A∩B)−n(B∩C)−n(C∩A) +n(A∩B∩C) (����) 4�̏W���̗v�f�̌�
n(A∪B∪C∪D)
(3)�@�ׂ��W���i�����W���̑����j=n(A)+n(B)+n(C)+n(D) −n(A∩B)−n(A∩C) … −n(C∩D) +n(A∩B∩C)+n(A∩B∩D) … +n(B∩C∩D) −n(A∩B∩C∩D) (�⑫����) ��W����A���g��A�̕����W���Ƃ��闝�R (�⑫����) �L���W���Ɩ����W���̈Ⴂ |
(1)�@�W��A�̗v�f�̌���\���L��n(A)
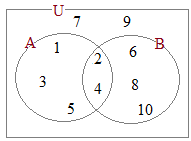 �@�W��A�̗v�f�̌����C�L��n(A)�ŕ\���܂��D
�@�W��A�̗v�f�̌����C�L��n(A)�ŕ\���܂��D�y��z �@10�ȉ��̐��̐����S�̂̏W����U�C���̂�����5�ȉ��̐����̏W����A�C�����̏W����B�ŕ\���Ƃ� A={1, 2, 3, 4, 5}������n(A)=5 B={2, 4, 6, 8, 10}������n(B)=5 A��B�̋��ʕ����́CA∩B={2, 4}������n(A∩B)=2 A��B�̘a�W���́CA∪B={1, 2, 3, 4, 5, 6, 8, 10}������n(A∪B)=8
(2)�@�W���̗v�f�̌��Ɋւ���藝
�y�����z
�@�L���W��A, B�̗v�f�̌��ɂ��� (2.1) ��ʂɎ��̊W�����藧�D n(A∪B)=n(A)+n(B)−n(A∩B) (2.2) ���ɁCA∩B=∅�i��W���j�̂Ƃ� n(A∪B)=n(A)+n(B) 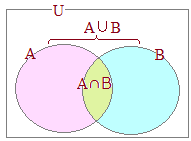 �i����j
�i����j(2.1)← A∪B�̗v�f�̌��𐔂���Ƃ��ɁCA�̌���B�̌��𑫂��ƁCA∩B�̌���2�d�ɐ����Ă��܂����ƂɂȂ邩��CA∩B�̌���1�����Ȃ���Ȃ�Ȃ��D (2.2)← A∩B=∅���Ȃ킿n(A∩B)=0�̂Ƃ��́CA�̌���B�̌���P���ɑ����悢�D |
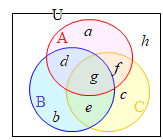 �i����j
�i����j (1)����E�}1�̂悤��
(1)����E�}1�̂悤��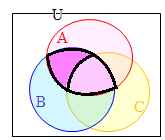 (4)�ɂ��
(4)�ɂ��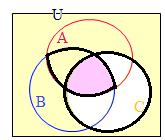 (5)�ɂ��
(5)�ɂ��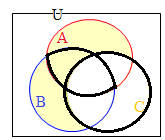 �E�}������Ε�����悤��
�E�}������Ε�����悤��
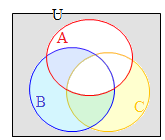 ���E�}�ɂ���Ċm���߂���
���E�}�ɂ���Ċm���߂���
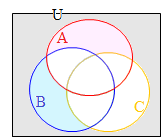 ���E�}�ɂ���Ċm���߂���
���E�}�ɂ���Ċm���߂���
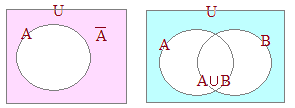
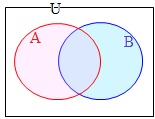 �@���Z���w�ł́C�W�������̂悤�Ȑ}�ŕ\���D
�@���Z���w�ł́C�W�������̂悤�Ȑ}�ŕ\���D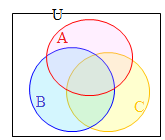 �@��������C�S�̏W���͒����`�ŕ\���C���̕����W�����~��p���ĕ\�����Ƃ������D
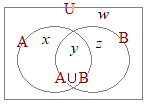
�@��������C�S�̏W���͒����`�ŕ\���C���̕����W�����~��p���ĕ\�����Ƃ������D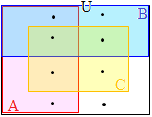 �@�����}�`���g���āC�R�̏W���́C�E�}�̐Ԑ���2�~2�~2=8�̗̈�ŕ\���ł���D�S�ڂ̏W��D��\������ɂ́C�E�}�̍��_��ʂ�����Ȃ��ŕȐ������悢�D�i�P�̗̈��ʂ̐�������CD�̐����������̂Ɩ������Ȃ����̂ɕ�������j
�@�����}�`���g���āC�R�̏W���́C�E�}�̐Ԑ���2�~2�~2=8�̗̈�ŕ\���ł���D�S�ڂ̏W��D��\������ɂ́C�E�}�̍��_��ʂ�����Ȃ��ŕȐ������悢�D�i�P�̗̈��ʂ̐�������CD�̐����������̂Ɩ������Ȃ����̂ɕ�������j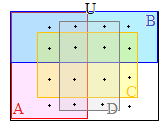 �@A,B,C,D�ɂ��24=16�ʂ�̗̈���邱�Ƃ��ł��邪�C�����5�ڂ̏W��E��\������ɂ́C�E�}�̍��_��ʂ�����Ȃ��ŕȐ������悢�D
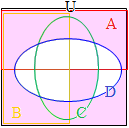
�@A,B,C,D�ɂ��24=16�ʂ�̗̈���邱�Ƃ��ł��邪�C�����5�ڂ̏W��E��\������ɂ́C�E�}�̍��_��ʂ�����Ȃ��ŕȐ������悢�D �@���̕��@�ɂ��CA,B,C,D,...�ƕK�v�Ȃ��������̏W����}�����邱�Ƃ��ł���.�iE��\���Ȑ��̕`�����͉��ʂ������j
�@���̕��@�ɂ��CA,B,C,D,...�ƕK�v�Ȃ��������̏W����}�����邱�Ƃ��ł���.�iE��\���Ȑ��̕`�����͉��ʂ������j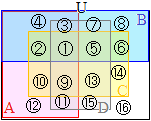
 (1)�@�E�}���玟�̎����l����
(1)�@�E�}���玟�̎����l����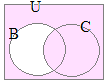
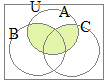 (3)�@�E�}���玟�̎����l����
(3)�@�E�}���玟�̎����l����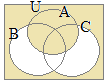 (4)�@�E�}���玟�̎����l����
(4)�@�E�}���玟�̎����l����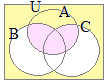 �i�ʉ��j
�i�ʉ��j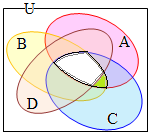 (5)�@�E�}���玟�̎����l����
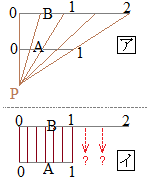
(5)�@�E�}���玟�̎����l���� �����̎�̖��������Ƃ��ɁC�E�}�̂悤�Ɂu�d�Ȃ�̂Ȃ��ŏ��P��
�����̎�̖��������Ƃ��ɁC�E�}�̂悤�Ɂu�d�Ȃ�̂Ȃ��ŏ��P��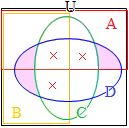 �E�}
�E�}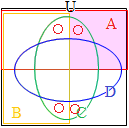 �E�}
�E�}
 �E�}
�E�}
 �E�}
�E�}
 ���a�̍�.�������w�Z.���w�̎���
���a�̍�.�������w�Z.���w�̎��� �L���Ȏ����̋�Ԃ�\���W��
�L���Ȏ����̋�Ԃ�\���W��