|
== 固有値,固有ベクトルの求め方 == → 携帯版は別頁
■固有値,固有ベクトルを求めるには
与えられた正方行列Aの固有値,固有ベクトルを求めるには,次のようにすればよい. (1) 行列Aの固有方程式
Aがn次正方行列のとき,固有値は[重解・虚数解も含めると]全部でn個ある.
(2) 各々の固有値を連立方程式
固有ベクトルの定数倍もまた固有ベクトルとなるので,固有ベクトルを答えるときは
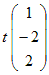 のように任意定数を付けた形で答えるとよい. のように任意定数を付けた形で答えるとよい.
例1
A=
(解答)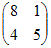 の固有値,固有ベクトルを求めよ. の固有値,固有ベクトルを求めよ.
(1) まず,固有方程式det 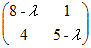 =0を解いて固有値を求める. =0を解いて固有値を求める.
(8−λ)(5−λ)−4=0
(2) 次に,各々の固有値に対応する固有ベクトルを求める.
λ2−13λ+40−4=0 λ2−13λ+36=0 (λ−4)(λ−9)=0 λ=4 , 9
(i) λ1=4を(A−λE)=に代入すると
ゆえに,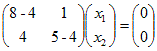 ←→ 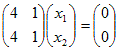 ←→ 4x1+x2=0 ←→ 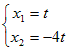 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )となるから, 固有ベクトルは 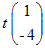 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )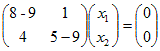 ←→ 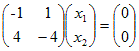 ←→ −x1+x2=0 ←→ 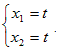 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )となるから, 固有ベクトルは 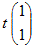 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )固有値λ1=4,固有ベクトル 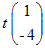 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )固有値λ2=9,固有ベクトル 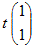 ( t は任意定数 , t≠0)…(答) ( t は任意定数 , t≠0)…(答)※この結果,行列 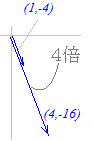 1つは
1つはのように方向が変わらず大きさが固有値λ1=4倍になります 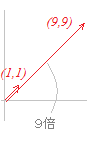 もう一つは
もう一つはのように方向が変わらず大きさが固有値λ2=9倍になります |
○ 与えられた正方行列Aに対して 零ベクトルでなく: ≠ …(*1) 方向が変わらない: A=λ …(*2) となるようなベクトルが存在するとき, λを行列Aの固有値,を固有ベクトルという. ○ (2)式を変形すると (A−λE)=…(*3) となるが,
一般に,与えられた正方行列Pに逆行列(P−1)が存在すれば(det(P)≠0のとき)
(*3)式が自明解でない解をもつ条件はdet(A−λE)=0になる.したがって,自明解でない解が存在するためには ←→ det(P)=0 ○ det(A−λE)はλのn次式になり,行列Aの固有多項式と呼ばれる. また,det(A−λE)=0を行列Aの固有方程式という.固有方程式はλのn次方程式になるので,重解や虚数解をもつ場合もすべて数えると全部でn個の解をもつ.
○ 解が不定となる連立方程式の解き方1
未知数が2個の連立方程式で2つの方程式が同じ式であるとき 例 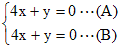 実際には,「4x+y=0を満たすx , yの組」はすべて解となる. 図形的には,「直線4x+y=0上の点 ( x , y )」はすべて解となる.…(C) 問題によっては(C)のように文章で答えてもよいが,以下において連立方程式の不定解の表し方を考える. (A)だけでは方程式が1つしかないので,1つの文字についてだけ解くことができもう一つの文字については解くことができないと考えるとよい.見た目で混乱しないように解くことをあきらめる方の文字は右辺に移項してかっこに入れてしまうとよい. 実質的にはこれで答えになっているが,もともと未知数が2個あったのに対して,この形ではyだけに「ひいき」していてxを「安っぽく」扱っているように見えるので,どちらにも偏らない第3の変数tを導入して,次のように表すと「見た目にもスマート」で「各々の変数を分けて表せる」. 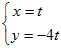 この解をベクトルの形式で表すと 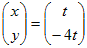 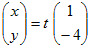 [注] (A)式をx=… の形にしてもよいが,その場合は途中経過と結果に分数が残り「見た目がスマートではない」のでこの形を好む解答者や採点官はあまりいない.(数学的にはまったく問題ない.) 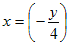 ⇒ ⇒ 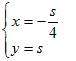 ⇒ ⇒ 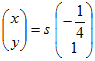 |
|
例2
A=
(解答)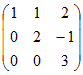 の固有値,固有ベクトルを求めよ. の固有値,固有ベクトルを求めよ.
(1) まず,固有方程式det 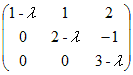 =0を解いて固有値を求める. =0を解いて固有値を求める.
(1−λ)(2−λ)(3−λ)+0·0·2+0·1·(−1)−(1−λ)·(−1)·0−0·1·(3−λ)−0·2·(2−λ)=0
(2) 次に,各々の固有値に対応する固有ベクトルを求める.
(1−λ)(2−λ)(3−λ)=0 λ=1 , 2 , 3
(i) λ1=1を(A−λE)=に代入すると
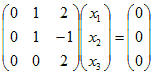 0x1=0は,どんな実数x1についても成り立つから,x1=t ( t は任意定数 , t≠0 ) 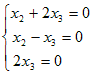 ←→ 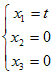 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )となるから, 固有ベクトルは 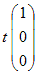 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )
(ii) λ2=2を(A−λE)=に代入すると
ゆえに,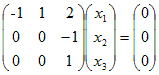 ←→ 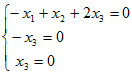 ←→ 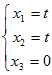 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )となるから, 固有ベクトルは 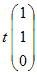 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )
(iii) λ3=3を(A−λE)=に代入すると
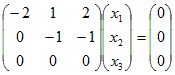 ←→ 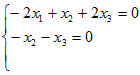 ←→ 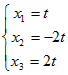 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )となるから, 固有ベクトルは 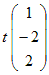 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )固有値λ1=1,固有ベクトル 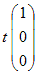 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )固有値λ2=2,固有ベクトル 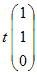 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )固有値λ3=3,固有ベクトル 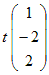 ( t は任意定数 , t≠0)…(答) ( t は任意定数 , t≠0)…(答)
|
○ 解が不定となる連立方程式の解き方2
未知数が3個の方程式2つのときも上と同様にして「1つの文字について解くのをあきらめる」とよい. 例 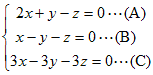 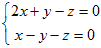 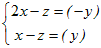 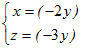 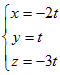 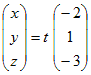
○ 解が不定となる連立方程式の解き方3
条件式がない変数は任意の値をとることができる. 例 (i)において未知数がx1 , x2 , x3でx2=0 , x3=0という解が得られたとき,x1は制限条件が何もない.このとき,x1は任意定数になる.この事情を中学校で習った直線の方程式で思い出してみると.点(3 , 0)を通りx軸と垂直な直線は次の図のような点を通っている. 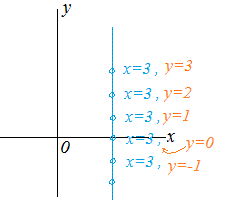 方程式では制限のないものは書かないので,この直線の方程式はx=3と書く. 逆に,方程式がx=3であるということはyは任意の値をとれるということを表している. x=3 ←→ x=3,yは任意 ←→ ( 3 , t )で表される点はすべて ←→ x=3, y=t (なお,この直線は原点を通らないので,(x,y)=t(... , ...)の形には書けない) 以上の簡単な復習から分かるように,左の連立方程式において,未知数がx1 , x2 , x3でx2=0 , x3=0という条件になるということは,x1には条件が指定されていないということで
x1は任意定数
ということになる.x2=0 x3=0 したがって, 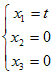 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )が解となる. |
|
■問題■ 次の行列の固有値,固有ベクトルを求めよ.
(1) A= 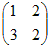 (2) A= 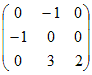 |
(解答) (1) 固有値−1,固有ベクトル 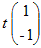 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )固有値4,固有ベクトル 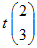 ( t は任意定数 , t≠0 ) ( t は任意定数 , t≠0 )(2) (※成分に分けて書くと) 固有値2,固有ベクトルx1=0, x2=0, x3=t 固有値−1,固有ベクトルx1=t, x2=t, x3=−t 固有値1,固有ベクトルx1=−t, x2=t, x3=−3t (いずれも,t は任意定数 , t≠0 ) |