|
■番号札のもらい方《解説》
【例1】
「同質の赤玉3個,青玉2個を一列に並べる方法は何通りあるか」という問題を組合せで考えてみます. 次の図で青線よりも上のような並べ方は,「並べた玉を動かす」という考え方以外に,「受付で番号札をもらう」という考え方でもできます. 赤組は玉を3個並べるので,受付で番号札を3枚もらいます.青組は番号札を2枚もらいます.番号札には,座席が書かれていて,1番の番号札をもらえば1番のところに並べる,2番の番号札をもらえば2番のところに並べる・・・というように決めます.
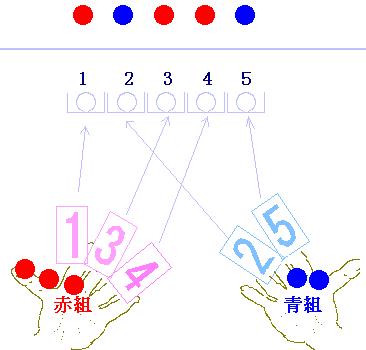 結局,同質の赤球3個,青玉2個を一列に並べる方法は,1から5までの番号札のうち赤が行き先の番号札3枚をもらえば決まります.(青の行き先は残り2か所で,これは赤が決まれば自動的に決まります.) だから5C3=10通りです.・・・(答) 青の行き先を先に決めても同じことになります:1から5までの番号札から青の行き先の番号札2枚をもらう方法は 5C2=10通りです. (このとき赤の行き先は,残りの3か所です.) このように,「並べ方の問題」なのに「組合せ」で解けるのは,番号札の組合せが並べ方を表しているからです.
【例2】
同質の赤球3個,青玉2個,黒玉2個を一列に並べる方法は何通りありますか.  このように考えると,問題の並べ方は,1から7の7枚の番号札のうち,赤の行き先を3枚、残りから青の行き先を2枚,(その残りは黒の行き先)というように番号札をもらう方法に等しいので,
【例3】
10円硬貨を6回投げるとき,表が3回出るのは何通りありますか. ・・・・・・・・ ・・・・・・・・ のように数えます. 一番上の図は,1から6の番号札のうち表組が1,2,3の3枚の番号札をもらった場合を表しています. ・・・・・・・ 一番下の図は,表組が4,5,6の3枚の番号札をもらった場合を表しています. 1から6までの6枚の番号札のうち,表の行き先の番号札3枚をもらう方法(表の行き先を決めたら,残りは自動的に裏に決まる)は 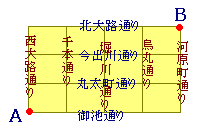 【例4】
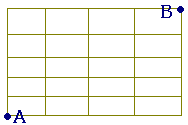
【例4】右図のような街路があるとき,A地点からB地点へ最短経路で行く方法は何通りありますか. 同じものがあるときの順列で考える方法もありますが,組合せでは次のように考えることができます. 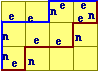
右の図で,北へ進むことをnで,東へ進むことをeで表すと,青色の順路はnneenee,茶色の順路はeneenenとなります. どの順路もnが3個,eが4個あります.青色の順路はnが1,2,5の番号札をもらった場合に対応します.茶色の順路は,nが2,5,7の番号札をもらった場合に対応します. このように,1から7番のうちでnの現れる番号を3枚もらえば順路が決まります. |