• 定数
e=2.18 ···を底とする指数関数を使うと,微分の計算が簡単になる.
 \( \displaystyle y=e^x\hspace{3px}\rightarrow\hspace{3px}y'=e^x \)
\( \displaystyle y=e^x\hspace{3px}\rightarrow\hspace{3px}y'=e^x \) …(1)
(この公式の証明は,このページの下の方にあります.先に公式の使い方の練習をします.)
底が
e以外の数の場合には,微分の計算は少しややこしくなる.
&chco=0000ff) \( \displaystyle y=a^x\hspace{3px}\rightarrow\hspace{3px}y'=a^x\log_ea\hspace{5px}(a\gt 0,\hspace{2px}a\ne 1) \)
\( \displaystyle y=a^x\hspace{3px}\rightarrow\hspace{3px}y'=a^x\log_ea\hspace{5px}(a\gt 0,\hspace{2px}a\ne 1) \) …(2)
底が
e以外のときは,
eに直して計算すると簡単になる.そのために,次の公式を使う.
 \( \displaystyle a=e^{\log a} \)・・・(3)
\( \displaystyle a=e^{\log a} \)・・・(3)
↑右辺の対数をとると,
=\log a&chco=aa4422) \( \displaystyle \log(e^{\log a})=\log a \)
\( \displaystyle \log(e^{\log a})=\log a \)となるから,右辺は
aに等しい.
そこで,
 \( \displaystyle a^x=e^{x\log a} \)
\( \displaystyle a^x=e^{x\log a} \)
\apos=\log a\cdot e^{x\log a}=a^x\cdot \log a&chco=aa4422) \( \displaystyle (a^x)'=\log a\cdot e^{x\log a}=a^x\cdot \log a \)
\( \displaystyle (a^x)'=\log a\cdot e^{x\log a}=a^x\cdot \log a \)になる.
(3)の変形が分からない場合は,次のように考えてもよい.
底は底,指数形と対数形で,中と外が入れ替わる
対数の定義:
 \( \displaystyle b \)
\( \displaystyle b \) \( \displaystyle =\log \)
\( \displaystyle =\log \) \( \displaystyle _e \)
\( \displaystyle _e \) \( \displaystyle a \)
\( \displaystyle a \)
 \( \displaystyle \Longleftrightarrow \)
\( \displaystyle \Longleftrightarrow \) \( \displaystyle e \)
\( \displaystyle e \) \( \displaystyle ^b \)
\( \displaystyle ^b \) \( \displaystyle = \)
\( \displaystyle = \) \( \displaystyle a \)
\( \displaystyle a \)
同じものは同じものに等しいから:
 \( \displaystyle \textcolor{red}{\log_e a}=\textcolor{black}{\log}\textcolor{green}{_e}\textcolor{blue}{a} \)
\( \displaystyle \textcolor{red}{\log_e a}=\textcolor{black}{\log}\textcolor{green}{_e}\textcolor{blue}{a} \)
 \( \displaystyle \Longleftrightarrow \)
\( \displaystyle \Longleftrightarrow \)
 \( \displaystyle \textcolor{green}{e}^\textcolor{red}{{\log_ea}}=\textcolor{blue}{a} \)・・・(3)
\( \displaystyle \textcolor{green}{e}^\textcolor{red}{{\log_ea}}=\textcolor{blue}{a} \)・・・(3)
• 数学Ⅱでは,様々な底の値を使うが,微分積分では,ほとんどの場合「自然対数の底」
eを使う.
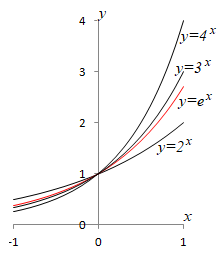
 (1)の解説
(1)の解説
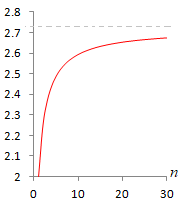
 自然対数の底(ネイピア数)
自然対数の底(ネイピア数)