|
はじめに
初等整数論には,問題の意味は小中学生でも分かるが,専門家でも証明できていない未解決問題が多くあります.3n+1問題(コラッツ予想)と呼ばれる問題もその1つです.この問題は,多くの数学愛好家が取り上げており,英語で書かれたweb記事が多数ありますが,多過ぎて調べ尽くすことは無理ですので,誰か他の人が既に書いていることと重なるかもしれませんが,以下の内容は,この教材の管理人が勝手に考えたものです. 専門家のチェックを受けていませんので,間違いがあるかもしれませんが,管理人なりの備忘録も兼ねています.
3n+1問題(コラッツ予想)とは
任意の正の整数nに対して(Ⅰ) nが奇数ならば3倍して1を加える. (Ⅱ) nが偶数ならば2で割る. という操作を繰り返して,1になったら終了とする. 1930年代にコラッツは,どんな正の整数から始めても上記の操作を繰り返せば1になると予想したが,この予想は証明も反証もできていない未解決問題となっている.(3n+1問題とも呼ばれる) 【例】 ≪3から始めると≫ 3→10→5→16→8→4→2→1 (7回の操作で1になる) ≪11から始めると≫ 11→34→17→52→26→13→40→20→10→5→16 →8→4→2→1 (14回の操作で1になる) ≪35から始めると≫ 35→106→53→160→80→40→20→10→5→16 →8→4→2→1 (13回の操作で1になる) |
中には非常に長い経過をたどるものがあり,27から始めると111回,55から始めると112回で1になる. ≪27から始めると≫ 27 →82 →41 →124 →62 →31 →94 →47 →142 →71 →214 →107 →322 →161 →484 →242 →121 →364 →182 →91 →274 →137 →412 →206 →103 →310 →155 →466 →233 →700 →350 →175 →526 →263 →790 →395 →1186 →593 →1780 →890 →445 →1336 →668 →334 →167 →502 →251 →754 →377 →1132 →566 →283 →850 →425 →1276 →638 →319 →958 →479 →1438 →719 →2158 →1079 →3238 →1619 →4858 →2429 →7288 →3644 →1822 →911 →2734 →1367 →4102 →2051 →6154 →3077 →9232 →4616 →2308 →1154 →577 →1732 →866 →433 →1300 →650 →325 →976 →488 →244 →122 →61 →184 →92 →46 →23 →70 →35 →106 →53 →160 →80 →40 →20 →10 →5 →16 →8 →4 →2 →1 ≪55から始めると≫ 55 →166 →83 →250 →125 →376 →188 →94 →47 →142 →71 →214 →107 →322 →161 →484 →242 →121 →364 →182 →91 →274 →137 →412 →206 →103 →310 →155 →466 →233 →700 →350 →175 →526 →263 →790 →395 →1186 →593 →1780 →890 →445 →1336 →668 →334 →167 →502 →251 →754 →377 →1132 →566 →283 →850 →425 →1276 →638 →319 →958 →479 →1438 →719 →2158 →1079 →3238 →1619 →4858 →2429 →7288 →3644 →1822 →911 →2734 →1367 →4102 →2051 →6154 →3077 →9232 →4616 →2308 →1154 →577 →1732 →866 →433 →1300 →650 →325 →976 →488 →244 →122 →61 →184 →92 →46 →23 →70 →35 →106 →53 →160 →80 →40 →20 →10 →5 →16 →8 →4 →2 →1
コンピュータを使って,非常に大きな整数まで成り立つことが確かめられている.
[2009年現在で5×:260(19桁の整数)まで調べられている:wikipedia] 非常に大きな数まで成り立つことは,たぶん正しいだろうなと思ってもらうことにとって有利な材料であるが,伝統的な数学が認める証明にはならない. 整数の未解決問題には,数学的には真偽が決まらないが,コンピュータを使って非常に大きな数まで正しいと言えるものが多い.
■3n+1問題(コラッツ予想)■
(*) どんな正の整数から始めても,上記の(1)(2)の操作を有限回繰り返せば1になる. (*1) どんな正の整数から始めても,同じ数字に戻って来ることはない. (*2) どんな正の整数から始めても,限りなく大きくなることはない. |
次の図は,3n+1の操作でできる数字の樹形図(以下ツリー1と略す)です.スマホで表示できるサイズにしているので,必要に応じてズームイン(拡大)して見てください.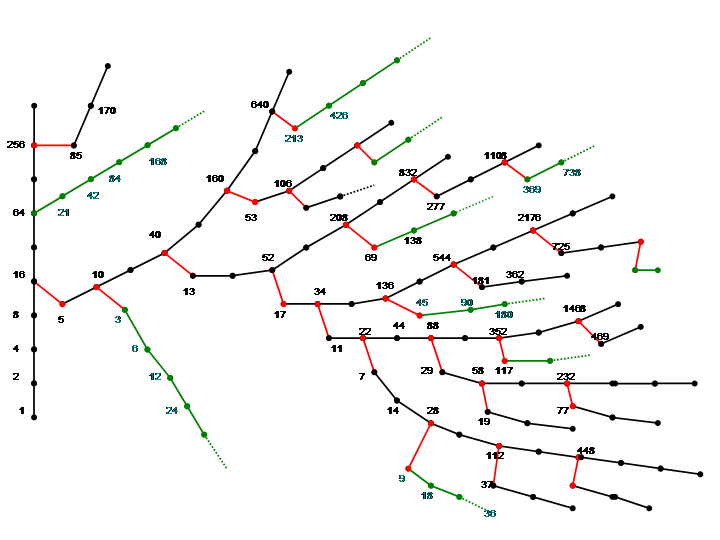 -図1-
■3n+1問題の書き換え(*3)■
これが証明できれば,3n+1問題は解決してしまうが,・・・.ツリー1にはすべての自然数が1回ずつ登場する このように,問題の核心については証明できなくても,数字の並びについて,幾つか言えることはある.
(A)どの数にも2n倍してできる無限に長い項の列がある
ツリー1ではこの列を黒線で示した.
例えば,5の上には
5←10←20←40←80←160←320←… と連なる数の列がある. また,11の上には 11←22←44←88←176←352←… と連なる数の列がある. これは「偶数ならば2で割る」というルールから逆算すれば明らかである. これにより,ある数nから始めたときに,1万回の操作を要する数nというように,与えられた操作回数になる「偶数」nは直ちに見つけることができる. 210000 他に,例えば5の下には5つのステップがあるから 5×29995 また,例えば3の下には7つのステップがあるから 3×29993 も10000回で1に至る. |
(B) 3×(奇数)の上に立つ幹は枝分かれしない.
ツリー1ではこの線を緑線で示した.
例えば,3の上には
3←6←12←24←48←96…←3×2n と連なる数の列がある. また,9の上には 9←18←36←72←144←288←…←9×2n と連なる数の列がある. しかし,3の倍数である数aが枝分かれしていれば,a=3x+1となるはずのところが,aが3の倍数なのだから,矛盾になる. したがって,3×(奇数)の上には×2nでできる1本の数列だけがある.  (C) ツリー1はシダ類植物の葉のように,相似図形になっている.
(C) ツリー1はシダ類植物の葉のように,相似図形になっている.
10←20←40←80←160←320←…
に対して↑↑13←26…↑53←106← 3←6←12←24…
28←56←112←224←448←896←…
を比較してみると↑↑37←74…↑149←298← 9←18←36←72… a=10とa=28が対応している. |
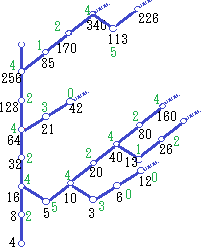 右の図は,ツリーの一部を示したもので,黒字は元の数,緑字は6で割ったときの余りです.
右の図は,ツリーの一部を示したもので,黒字は元の数,緑字は6で割ったときの余りです.例えば,16を見ると前述(A)で述べたように,どの数字にもあるように×2mの上に伸びる枝がありますが,5につながる分岐もあります. 3n+1問題の元の約束
(Ⅰ) nが奇数ならば3倍して1を加える.
において,この約束の流れに沿って次の数を求めるのを,以下においては「順方向」「上から下へ」と言い,その逆を「逆方向」「下から上へ」と言うことにする.(Ⅱ) nが偶数ならば2で割る.
(D)
順方向にmからnを求めるとき,mが奇数のときn=3m+1とするのだから,[1] 6で割って4余る数(4 mod 6)に分岐があり,他の項にはない. ア) n=6k+4 → 分岐がある. イ) n=6k, 6k+1, 6k+2, 6k+3, 6k+5 → 分岐はない. [2] 奇数は,この分岐から逆方向にたどった片方の枝の1つ目の項にあり,他の項にはない.
m=2k+1
n=3m+1=3(2k+1)+1=6k+4 |
(E)
[1] 6で割って4余る数(4 mod 6)を,もう少し詳しく分けると,
ア) 18で割って4余る数(4 mod 18)
の3種類に分かれる.イ) 18で割って10余る数(10 mod 18) ウ) 18で割って16余る数(16 mod 18) [2] イ)につながる奇数の枝には3の倍数が並び,その枝は再分岐しない…(B)で述べた性質 ア)ウ)につながる奇数の枝は再分岐がある. 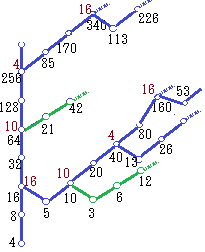 右の図で茶色字は18で割ったときの余りです.
[1]
右の図で茶色字は18で割ったときの余りです.
[1]イ) 18k+10=3m+1 のときは m=6k+3 となって,mが3の倍数となるから,(B)の性質により再分岐のない一本枝になります. (右図の3, 21がこれに該当します) ア) 18k+4=3m+1 のときは m=6k+1 となり,右図の85, 13のように再分岐のある枝になります. ウ) 18k+16=3m+1 のときは m=6k+5 となり,右図の53, 113のように再分岐のある枝になります. |
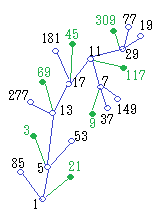 -図2- ツリー2において,1つの項(例えば5)から逆順に1つ進んだところにある項を衛星と呼ぶことにすると,5の衛星には3,13,53,...などがあります.また,13の衛星には,17,69,277,...などがあります.正確には,各々無限個ありますが,書き切れないので3個ずつ表示しています.
(F)
1) 例えば,5の1つの衛星3に対して,3×4+1=13, 13×4+1=13, 13×4+1=53,…のように前の項を4倍して1加えると次の項になります.1) ある項xの1つの衛星をanとすると,その次に大きい衛星はan+1=4an+1で求めることができます. 2) 1)の漸化式から一般項を求めると,ある項xの衛星は または で求められます. これは,ツリー1の図でx=3とおくと
10=3x+1
のようにx → 4x+1の繰り返して次の衛星が得られることから分かります.20=(3x+1)×2 40=(3x+1)×4 |
2) 例えば,x=5の衛星anに対しては,次の漸化式から一般項を求めることができます.
an+1=4an+1
an=3, 13, 53, …
により,a1=3, b1=10 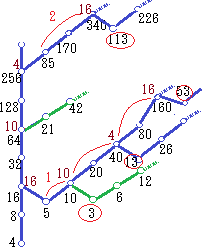 右図のように,5から逆順に見て奇数番目の項から3が分岐している場合には,上記のように2n−1乗になりますが,85から逆順に見て偶数番目の項から113が分岐しているような場合には,2n乗になります
右図のように,5から逆順に見て奇数番目の項から3が分岐している場合には,上記のように2n−1乗になりますが,85から逆順に見て偶数番目の項から113が分岐しているような場合には,2n乗になります
|
|
■3n+1問題の書き換え■
これが証明できれば,3n+1問題が証明できたことになると考えられるが,管理人にはもちろん証明できない.図2のツリー2にはすべての奇数が1回ずつ登場する ただし,もう少していねいに言うと,ツリー2にすべての正の奇数が「もれなく」「重複なく」登場するということのうちで,難しいのは「もれなく」の方で,「重複なく」登場するのは自明だと考えられる. というのは,3n+1問題において次の数を求める手順
(Ⅰ) nが奇数ならば3倍して1を加える.
は一意的なので,ある数が等しければ順方向に進んだときにそれ以下のすべての項も等しくなる.
(Ⅱ) nが偶数ならば2で割る.
an=bnならば
これは同じものを2回書いているだけになるから,重複して登場することはないと言えるでしょう.k=1,2,3,…についてak=bk したがって,難しいのは,すべての奇数が「もれなく」登場することの証明です. 与えられた奇数(例えば27)が登場する枝を具体的に示せたら完璧ですが,それが示せなくとも,このツリー2に何らかの奇数が欠如していると仮定して矛盾を示す(背理法)でもOKです. |
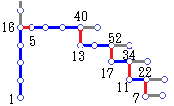 (G) 興味ある性質
(G) 興味ある性質右図(ツリー1の部分)において,与えられた整数は途中経路の分岐となっている項で表すことができます. 例えば,整数7が与えられたとき,3n+1問題の順方向に進むと,途中の分岐点,22,34,52,40,16を通ります.このとき,7は次のような(有限)乗積と等しくなります. この式は単なる分数計算で証明できます.すなわち 最後の 最後の このとき,7から11もしくは22を,11から17もしくは34を,…を見つける方法は,3n+1問題において次の数を求める手順の通りに行いますので,この式は3n+1問題の約束を復唱したものにすぎません. ただし,このように書くと,3n+1問題はそれと同値な次の形に書き替えられることになります. すべての奇数は のように(有限)乗積で書ける. さらに,n<20000までの経験則としていえば,右端の2の指数pと3の指数qについては, |
|
〇上記の性質を,n=7の場合を使って解説 n=7からスタートして,3n+1問題の約束に従って,途中の値を求めていくと,7→22→11→34→17→52→26→13→40→20→10→5→16 →8→4→2→1 となり,3を掛けて1加える操作を5回,2で割る操作を11回,合計16回の操作が行われます. この途中経過に登場する各々の値に対して
 |
〇同様にして,n=9の場合を使って解説 n=9からスタートして,3n+1問題の約束に従って,途中の値を求めていくと,9→28→14→7→22→11→34→17→52→26→13→40→20 →10→5→16→8→4→2→1 となり,3を掛けて1加える操作を6回,2で割る操作を13回,合計19回の操作が行われます. この途中経過に登場する各々の値に対して
 |
|
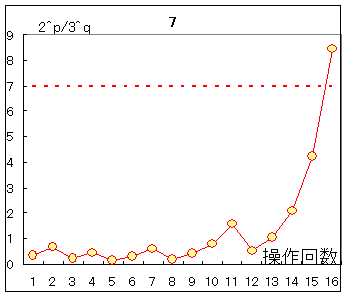
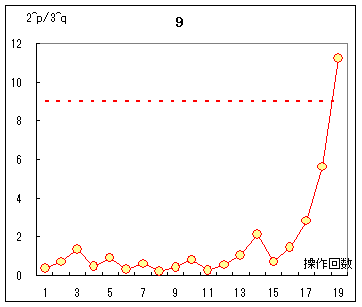
〇同様にして,n=27の場合を使って解説 n=27の場合は,途中経過が非常に長くなるので,表を省略してグラフのみ示すと,次のようになります. 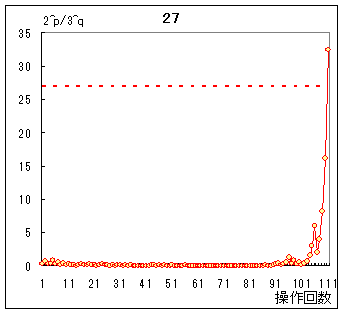 〇nが大きくなると,p,qが大きくなる訳ではなく,n=28では次のように比較的短い途中経過をたどり,p=13,q=5の合計18回の操作で終了します. 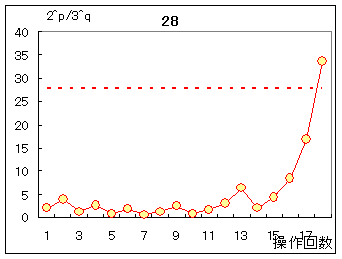 |
【要点】
例えばn=7のとき,(p,q)=(6,2),(11,5),(14,7),(22,12),(25,14),…などが与えられた正の整数nからスタートして,3n+1問題の約束に従って1に帰着するまでに,2で割った回数をp,3を掛けて1加えた回数をqとすると が成り立つ. 逆は言えない.すなわち, この1つを判別する方法があれば,3n+1問題が肯定的に解けたというのと同じことになるが,筆者にはまだ解けていない. 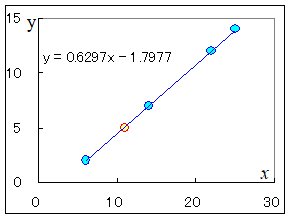 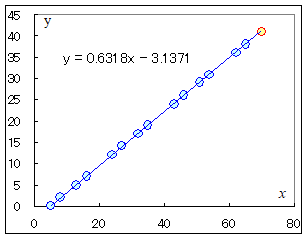 |
|
■100以下の整数のうちで,操作回数が多い数には次のようなものがある. これらのどの数についても,上記の要点は成り立つ.
|
■1000以下の整数のうちで,操作回数が多い数には次のようなものがある. これらのどの数についても,上記の要点は成り立つ.
|
|
(G)のまとめ 正の整数nが与えられたとき,3n+1問題の約束に従って計算して,2で割る操作がp回,3を掛けて1加える操作がq回,合計p+q回の操作が必要であるとすると,p, qの組は を満たす. (1) 20000までの整数については実験的に確かめられる. (2) 定数Rの理論的な根拠はよく分からないが,n<20000での実測値である. |
|
(H) 整数nとp, qとの対応 この表で,1つのマス目を見たとき,その数が「偶数なら上に1つ進む」「奇数なら左に1つ進む」という約束で進みます. 実際には,上に2回以上続けて進むことはありますが,左に2回以上続けて進むことはありません. この表の中のどのマス目からスタートしても,最終的に左上端の1にたどり着きます. 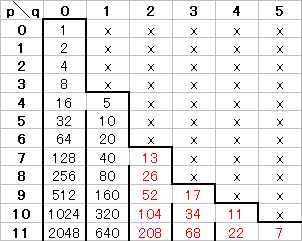 表1,2,3では,赤で示した部分が異なっており,例えばp=7, q=2のマス目には,表1では13があり,表2では12があります. また,奇数は各列の上端にのみあるように見えますが,表を重ねてみると,例えばq=2の列で,表3ではp=5に3があり,表1ではp=7に13があり,表3ではp=9に53があります. |
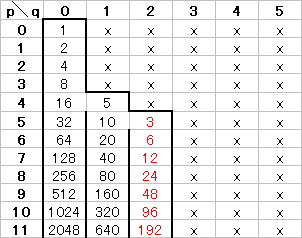 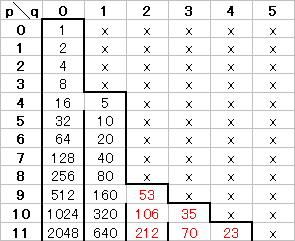 例えばq=1の列を見ると,p=4のときn=5があり,そこから2行下には4n+1=21,さらに2行下には4n+1=85,…と奇数が並びます. q=2の列では,n=3に対して4n+1=13,さらに4n+1=53,…だけでなく,n=113に対して4n+1=453,…,さらにn=227に対して4n+1=909,…と見えている範囲だけで3つの系列があります. |
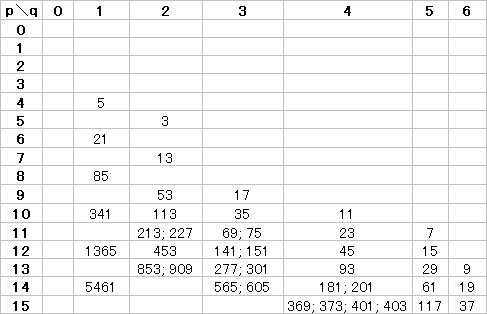 下の方は空白ではなく,数字が大きすぎて表示できないから書いてないということで,対角線の上の部分とは事情が異なります. |
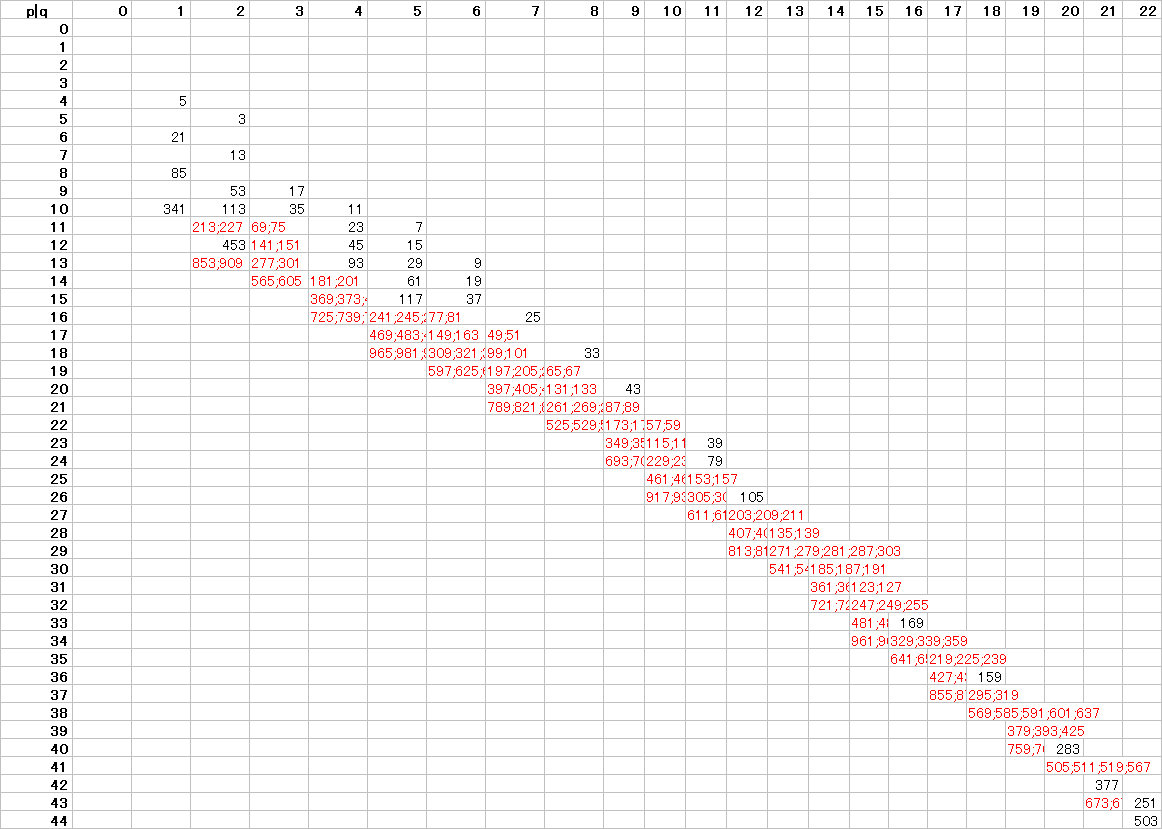 |
(I) 3n+1問題の逆方向に進んで任意の与えられた正の整数q番目の分岐(の次)の値を求める方法
(G)の項目で示した右図において,例えば7という項は5番目の分岐22の次にあります. 逆に,5番目の分岐(の次)にある項を1つ求めよという形の問題に答える方法を考えてみます. 以下の解説には,(G)の有限乗積,(D)の4 mod 6,(C)の相似図形の3つの内容を使います. (G)で述べたように,例えばn=7という項は,途中経路にある分岐点,22,34,52,40,16を使って次のように表すことができます. すなわち この式の右端の因数の この式の主要部分を左右逆に書いていくと となります.この書き方に沿って,5番目の分岐(の次)にある項を1つ求めてみます.(1つというのは,5番目の分岐は幾つもあるからです) |
(D)により,分岐は必ず 4 mod 6にあるので,右の掛け算表で4となる縦横を見ます. また,分岐後に掛けられるのは2nなので,2nの表も作っておきます.
1) 1番目の分岐を16に選びます.
64=26,256=28,1024=210などでもよいが,数字が小さい方が楽なので,16を選んだ
2) 2番目の分岐を考えます:分子は16=1=15=5×3になるから,mod 6 の掛け算表を使って,次の?に入る数を探します.
5×?≡4 (mod 6)となる数は 2 (mod 6)だから,表2により2, 8, ...が可能です.
5×2=10とすると,分子が9=3×3となって,3は次の分岐がないので,これを避けて8を選びます. |
|
3) 3番目の分岐を考えます:分子は39=13×3になるから,mod 6 の掛け算表を使って,次の?に入る数を探します.
13×?≡1×?≡4 (mod 6)となる数?は 4 (mod 6)だから,表2により4, 16, ...が可能です.
4) 4番目の分岐を考えます:分子は51=17×3になるから,mod 6 の掛け算表を使って,次の?に入る数を探します.小さい数の方が計算が楽なので,4を選びます.
17×?≡5×?≡4 (mod 6)となる数?は 2 (mod 6)だから,表2により2, 8, ...が可能です.
5) 5番目の分岐を考えます:分子は33=11×3になるから,mod 6 の掛け算表を使って,次の?に入る数を探します.小さい数の方が計算が楽なので,2を選びます.
11×?≡5×?≡4 (mod 6)となる数?は 2 (mod 6)だから,表2により2, 8, ...が可能です.
以上により,5番目の分岐の次にある(1つの)数は,次のように書けます.小さい数の方が計算が楽なので,2を選びます. 簡単な約分計算により,この式は次のように書けます. |
(J) 上記の(I)の手順で登場する奇数について,「同一の項が重複して登場しない」ことは背理法によって示せる この系列の中に登場する1つの項,例えば13が再び登場したとすると (1)を(2)に代入すると 左辺は2の倍数で右辺は2の倍数でないから(右辺は3の倍数で左辺は3の倍数でないから)矛盾 よって,同一の数が重複して登場することはない. |