== �O�p�� ==
 �y���3.1�z
�y���3.1�z
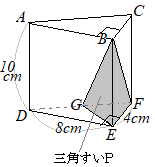
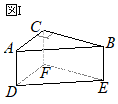
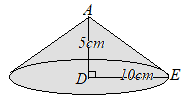
�@�E�̐}�̂悤�ɁC�_ A, B, C, D, E, F�_�Ƃ��C ��DEF=90�� �̒��p�O�p�` DEF���ʂ̂P�Ƃ���O�p��������B�� DF�̒��_�� G�Ƃ��C�S�_ B, E, F, G������ŎO�p�����o�����B
�@�� DE�̒����� 8cm�C�� EF�̒����� 4cm�C�� AD�̒����� 10cm�̂Ƃ��C���̊e�₢�ɓ����Ȃ����B
�@�Ȃ��C�e�₢�ɂ����āC�����̕����  \( \displaystyle \sqrt{\hspace{10px}} \) \( \displaystyle \sqrt{\hspace{10px}} \)���܂܂�Ă���Ƃ��́C�����L�������Ȃ����B�܂��C  \( \displaystyle \sqrt{\hspace{10px}} \) \( \displaystyle \sqrt{\hspace{10px}} \)�̒����ł��邾�����������R���ɂ��Ȃ����B
�@�@�O�p�����o�̑̐ς����߂Ȃ����B
�A�@��
�i�O�d��2017�N�������j
�O�p�` DEF�͒��p�O�p�`�ŁC ��DEF=90�� ������C���̖ʐς�
 \( \displaystyle \frac{8\times 4}{2}=16 \)(cm2) \( \displaystyle \frac{8\times 4}{2}=16 \)(cm2)
�O�p�` GEF�̖ʐς͂��̔���������
 \( \displaystyle 8 \)(cm2) \( \displaystyle 8 \)(cm2)
���ɁC�O�p�����o�̍��� EB=10(cm)
���������āC�O�p�����o�̑̐ς�
 \( \displaystyle \frac{1}{3}\times 8\times 10=\frac{80}{3} \)(cm3)…�i���j \( \displaystyle \frac{1}{3}\times 8\times 10=\frac{80}{3} \)(cm3)…�i���j
 �y���3.2�z
�y���3.2�z
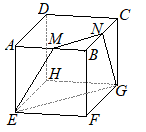
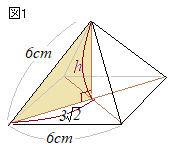
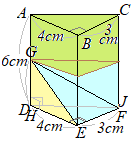
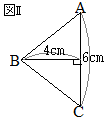
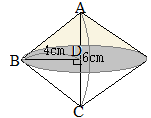
�@�E�̐}�̂悤�ɁC�P�ӂ̒����� 4cm�̗����̂�����C�� AB�̒��_�� M�C�� BC�̒��_�� N�Ƃ���B���̗����̂��S�_ M, E, G, N��ʂ镽�ʂłQ�̗��̂ɐ�B
�@���̂Ƃ��C����(1)�`(5)�̊e�₢�ɓ����Ȃ����B
(4)�@�Q�̗��̂̂����C���_ B���܂ޗ��̂̑̐ς����߂�B
(1)(2)(3)(5)�@��
�i���ꌧ2000�N�������j
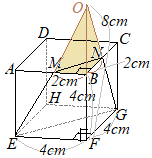
�@�E�}�̂悤�� EM�̉������C FB�̉������C GN�̉������͂P�_�Ō����D���̓_�� O�Ƃ���ƁC O-MBN, O-EFG�͂�������O�p���ɂȂ�D
�@�O�p�� O-EFG�̑̐ς�
\times 8=\frac{64}{3}) \( \displaystyle \frac{1}{3}\times(\frac{1}{2}\times 4\times 4)\times 8=\frac{64}{3} \)(cm3) \( \displaystyle \frac{1}{3}\times(\frac{1}{2}\times 4\times 4)\times 8=\frac{64}{3} \)(cm3)
�@�O�p�� O-MBN�̑̐ς�
\times 4=\frac{8}{3}) \( \displaystyle \frac{1}{3}\times(\frac{1}{2}\times 2\times 2)\times 4=\frac{8}{3} \)(cm3) \( \displaystyle \frac{1}{3}\times(\frac{1}{2}\times 2\times 2)\times 4=\frac{8}{3} \)(cm3)
�@�����̍������߂�}�`�̑̐ςɂȂ�
 \( \displaystyle \frac{64}{3}-\frac{8}{3}=\frac{56}{3} \)(cm3)…�i���j \( \displaystyle \frac{64}{3}-\frac{8}{3}=\frac{56}{3} \)(cm3)…�i���j
|
 �y���3.3�z
�y���3.3�z
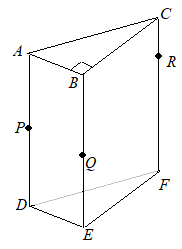
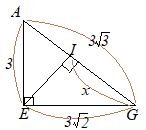
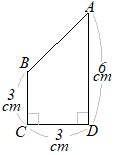
�@�E�̐}�́C��ʂ����p�O�p�`�ŁC���ʂ͂��ׂĒ����`�̎O�p�� ABC-DEF�ł���C ��ABC=90��, AB=4cm, BC=6cm, AD=12cm�Ƃ���B�܂��C�_ P, Q, R�͂��ꂼ��� AD, BE, CF��̓_�ŁC AP=6cm, BQ=7cm, CR=3cm�Ƃ���B���̂Ƃ��C����(1)�E(2)�̖₢�ɓ����Ȃ����B
(1)�@��
(2)�@�R�_ P, Q, R��ʂ镽�ʂł��̗��̂���ĂQ�ɕ�����Ƃ��C���_ E���ӂ��ނق��̗��̂̑̐ς����߂�B
�i���m��2000�N�������j
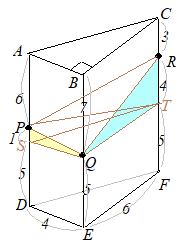
�E�}�̂悤�ɓ_ Q��ʂ� ��ABC�ɕ��s�ȕ��ʂ� AD, CF�̌�_�� S, T�Ƃ����Ƃ��C�O�p�� SQT-DEF�C�O�p���� PSQT�C�O�p���� PQTR�̂R�ɕ����đ̐ς����߂�Ƃ悢�D
�@��� ��ABC�̖ʐς́C 4×6÷2=12������C�O�p�� SQT-DEF�̑̐ς�
 \( \displaystyle V_1=12\times 5=60 \) \( \displaystyle V_1=12\times 5=60 \)
�O�p���� PSQT�� ��SQT=12���ʂƂ���ƁC PS=1�������ɂȂ邩��
 \( \displaystyle V_2=\frac{1}{3}\times 12\times 1=4 \) \( \displaystyle V_2=\frac{1}{3}\times 12\times 1=4 \)
�O�p���� PQRT�� ��QRT=6×:4÷2=12���ʂƂ���ƁC QS=4�������ɂȂ�D���̑̐ς́C���_�� P���� S�ɓ��ϕό`���Ă�����������C ��SQT=12���ʂƂ��C RT=4�������Ƃ���O�p�����Ɠ���
 \( \displaystyle V_3=\frac{1}{3}\times 12\times 4=16 \) \( \displaystyle V_3=\frac{1}{3}\times 12\times 4=16 \)
���������āC���߂闧�̂̑̐ς�
 \( \displaystyle V_1+ V_2+ V_3=80 \) \( \displaystyle V_1+ V_2+ V_3=80 \)(cm 3)…�i���j
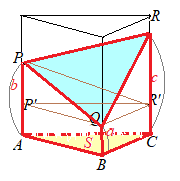
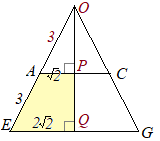
��ʂɁC��ʐς� S�̎O�p�����C�E�}�̂悤�ɒ�ʂ���̍������e�X a, b, c (a<b<c)�ƂȂ�悤�Ɏ߂ɐ����Ƃ��C���̗��� ABC-PQR�̑̐ς�
}{3}&chco=aa2200) \( \displaystyle V=\frac{S(a+ b+ c)}{3} \) \( \displaystyle V=\frac{S(a+ b+ c)}{3} \)
�����藧���܂��D�i�o����K�v�͂Ȃ��j
�i����j
�O�p�� ABC-P'QR'�̑̐ς� Sa
�O�p���� PP'QR'�̑̐ς� &chco=aa2200) \( \displaystyle \frac{1}{3}S(b-a) \) \( \displaystyle \frac{1}{3}S(b-a) \)
�O�p���� PQRR'�̑̐ς� P'QRR'�̑̐ςɓ��������� &chco=aa2200) \( \displaystyle \frac{1}{3}S(c-a) \) \( \displaystyle \frac{1}{3}S(c-a) \)
�����̘a��
%2B\frac{1}{3}S(c-a)=\frac{S(a%2B b%2B c)}{3}&chco=aa2200) \( \displaystyle Sa+\frac{1}{3}S(b-a)+\frac{1}{3}S(c-a)=\frac{S(a+ b+ c)}{3} \) \( \displaystyle Sa+\frac{1}{3}S(b-a)+\frac{1}{3}S(c-a)=\frac{S(a+ b+ c)}{3} \)
|
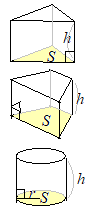 �y�v�_�z…�l�p���C�O�p���C�~���̑̐�
�y�v�_�z…�l�p���C�O�p���C�~���̑̐�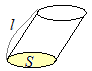 ���ȒP�Ȃ��Ƃ̂悤�Ɍ����܂����C��ʂƍ����Ƃ����p�ɂȂ��Ă���ꍇ�������̌������g���܂��D�Ⴆ�C�E�}�ɂ�����Sl�͂��̗��̂̑̐ςł͂���܂���D
���ȒP�Ȃ��Ƃ̂悤�Ɍ����܂����C��ʂƍ����Ƃ����p�ɂȂ��Ă���ꍇ�������̌������g���܂��D�Ⴆ�C�E�}�ɂ�����Sl�͂��̗��̂̑̐ςł͂���܂���D
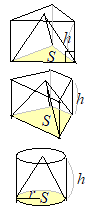 �y�v�_�z…�l�p���C�O�p���C�~���̑̐�
�y�v�_�z…�l�p���C�O�p���C�~���̑̐�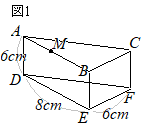
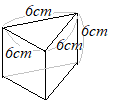
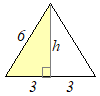 ��ʂ͂P�ӂ̒�����
��ʂ͂P�ӂ̒�����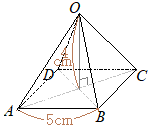
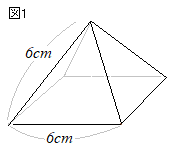
 ��ʂ͂P�ӂ̒�����
��ʂ͂P�ӂ̒�����
 �@��ʂ͂P�ӂ̒�����
�@��ʂ͂P�ӂ̒�����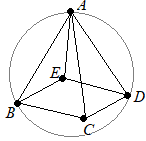
 ���
���

 �@�E�}�̂悤��
�@�E�}�̂悤��
 �E�}�̂悤�ɓ_
�E�}�̂悤�ɓ_ ��ʂɁC��ʐς�
��ʂɁC��ʐς�
 (�A)
�E�}�̂悤�Ȓf�ʂ��l����ƁC
(�A)
�E�}�̂悤�Ȓf�ʂ��l����ƁC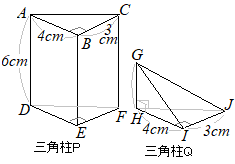
 �E�}�̂悤�ɁC�O�p��
�E�}�̂悤�ɁC�O�p��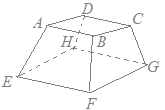
 �@
�@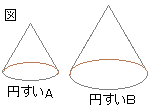
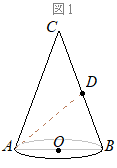
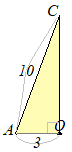
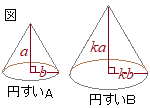 ���w�Z�ȗ��C�̐ϔ�͑�����̂R���Ɗo���܂����C���̖��̂悤�ȉ~�����̏ꍇ�ɁC���̌����̏ؖ��͎��̂悤�ɂȂ�܂��D
���w�Z�ȗ��C�̐ϔ�͑�����̂R���Ɗo���܂����C���̖��̂悤�ȉ~�����̏ꍇ�ɁC���̌����̏ؖ��͎��̂悤�ɂȂ�܂��D
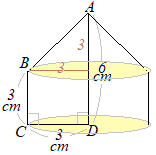 (�A)
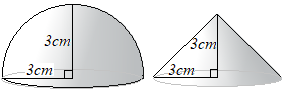
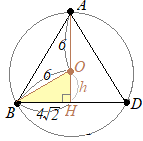
�E�}�̂悤�ɉ~���Ɖ~����g�ݍ��킹�����̂��ł���D
(�A)
�E�}�̂悤�ɉ~���Ɖ~����g�ݍ��킹�����̂��ł���D