|
■２点間の距離
■要点
※ ２点間の距離の公式では，三平方の定理を思い浮かべる．２点 A(x1 , y1 ) , B(x2 , y2 ) 間の距離 AB は (1) 横の長さは，ｘ座標の「差」にする．･･･２乗するから，一時的に負になっても気にしない． (2) 縦の長さは，ｙ座標の「差」にする．･･･２乗するから，一時的に負になっても気にしない． (3) a2=b2+c2 に当てはめて，斜辺の長さ a を求めると答えになる． |
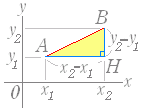 （解説）２点間の距離の公式は，三平方の定理を使って示すことができる． 右図において直角三角形 AHB の横の長さは AH=x2 - x1，縦の長さは BH=y2 - y1 だから，斜辺の長さ AB は，三平方の定理から で，２点 A(x1 , y1 ) , B(x2 , y2 ) 間の距離が求められる． ※ この公式は B の x 座標や y 座標が A の x 座標や y 座標よりも小さいときも成り立つ．（２乗するので，どちらの場合も正になる．） ※ AB が縦に並んでいるとき（ x1=x2 ) のとき）や，AB が横に並んでいるとき（ y1=y2 ) のとき）は直角三角形にならないが，AB は各々縦または横の長さとなって，この公式の結果は正しい． 要するに，この公式は常に成り立つ． |
|
問題 次の２点間の距離を求めなさい．（答は解答欄から選びなさい．） ［ルール］ (1) START (２回目からはNEXT)を押すと，１問表示されタイマーが動き始めます．（分からないときはHELPを押す．） (2) 正解したときに残っている「パン」の数が得点です． (3) 全部で10問あり，満点で10点×10=100点です． [第 問/全10問中]
|
※ 「魚」がジャンプする速さを調整するには，上のスケールで好みの目盛をクリック． （ドラッグではない．） |
|
|
|
|
［合計得点］ |
